11  Correlation structures

11.1 General Idea

Except for the random effects, we have so far assumed that residual errors are independent. However, that must not always be the case - we may find that residuals show autocorrelation.

Note

Correlation means that one variable correlates with another. Autocorrelation means that data points of one variable that are close to each other have similar values. This implies that autocorrelation is only defined if there is a “distance relationship” between observations.

Autocorrelation can always occur if we have a distance relationship between observations. Apart from random effects, where distance is expressed by group, common examples of continuous distance relationships include:

  • Random effects (distance = group)
  • Spatial distance.
  • Temporal distance.
  • Phylogenetic distance.

Here a visualization from Roberts et al., 2016 (reproduced as OA, copyright: the authors).

11.1.1 Models to deal with autocorrelation

If we find autocorrelation in the residuals of our model, there can be several reasons, which we can address by different structures.

Important

In the context of regression models, we are never interested in the autocorrelation of the response / predictors per se, but only in the residuals. Thus, it doesn’t make sense to assume that you need a spatial model only because you have a spatially autocorrelated signal.

  1. Autocorrelation can occur because we have a spatially correlated misfit, i.e. there is a trend in the given space (e.g. time, space, phylogeny). If this is the case, de-trending the model (with a linear regression term or a spline) will remove the residual autocorrelation. We should always de-trend first because we consider moving to a model with a residual correlation structure.

  2. Only after accounting for the trend, we should test if there is a residual spatial / temporal / phylogenetic autocorrelation. If that is the case, we would usually use a so-called conditional autoregressive (CAR) structures. In these models, we make parametric assumptions for how the correlation between data points falls off with distance. When we speak about spatial / temporal / phylogenetic regressions, we usually refer to these or similar models.

11.1.2 R implementation

To de-trend, you can just use standard regression terms or splines on time or space. For the rest of this chapter, we will concentrate on how to specify “real” correlation structures. However, in the case studies, you should always de-trend first.

To account for “real” autocorrelation of residuals, similar as for the variance modelling, we can add correlation structures

The following pages provide examples and further comments on how to do this.

Note

Especially for spatial models, both nlme and glmmTMB are relatively slow. Therea are a large number of specialized packages that deal in particular with the problem of spatial models, including MASS::glmmPQL, BRMS, INLA, spaMM, and many more. To keep things simple and concentrate on the principles, however, we will stick with the packages you already know.

11.2 Temporal Correlation Structures

To introduce temporal autoregressive models, let’s simulate some data first. The most simple (and common) temporal structure is the AR1 model, aka autoregressive model with lag 1. The AR1 assumes that the next data point (or residual) originates from a weighted mean of the last data point and a residual normal distribution in the form

\[ x_{t+1} = a \cdot x_t + (1-a) \cdot \epsilon \]

Let’s simulate some data according to this model

# simulate temporally autocorrelated data
AR1sim<-function(n, a){
  x = rep(NA, n)
  x[1] = 0
  for(i in 2:n){
    x[i] = a * x[i-1] + (1-a) * rnorm(1)
  }
  return(x)
}

set.seed(123)
obs = AR1sim(1000, 0.9)
plot(obs)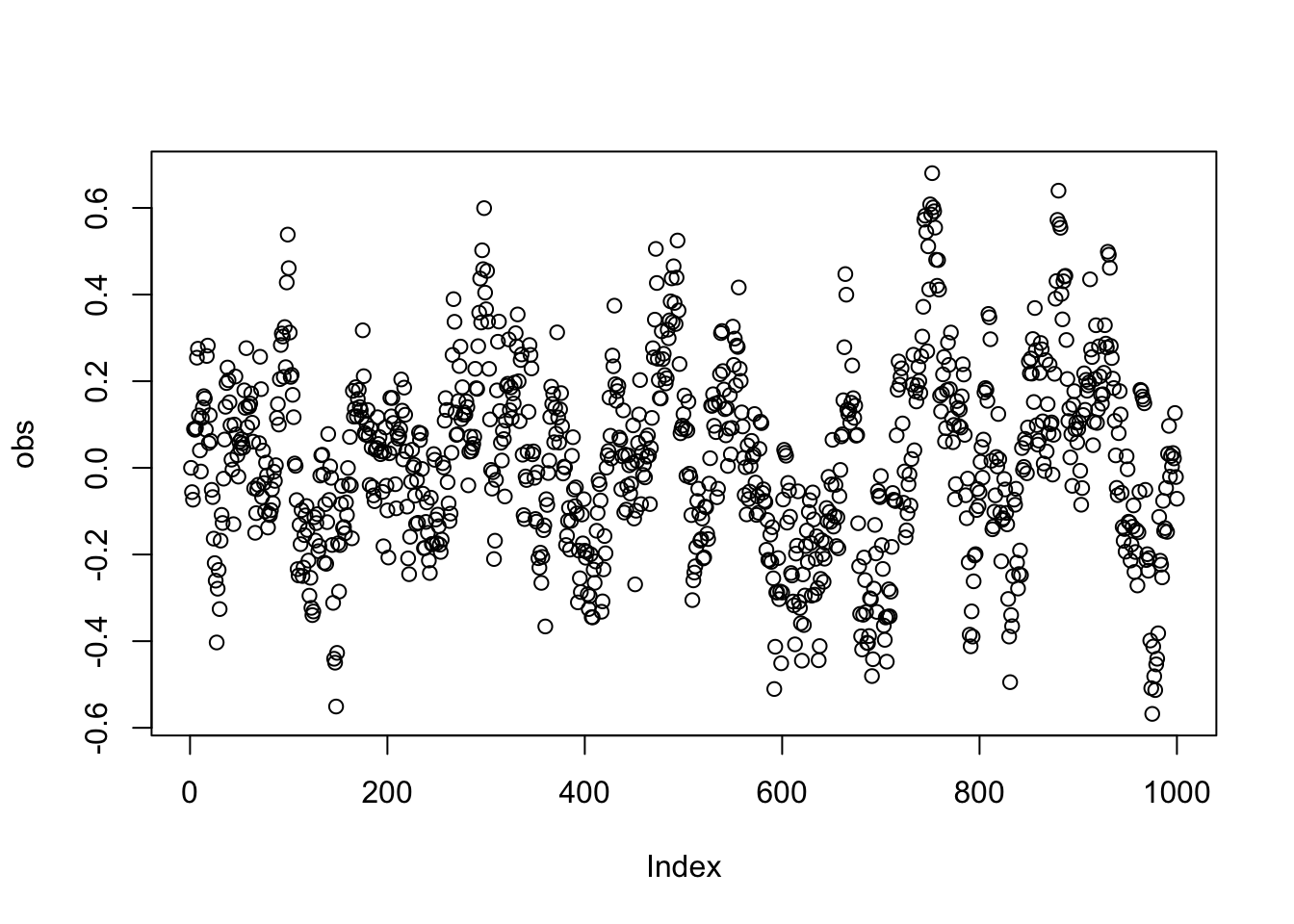

As we can see, we have a temporal correlation here. As we have not modeled / specified any further predictors, the correlation in the signal will transform directly in the correlations of the residuals if we fit a model:

fit = lm(obs~1)
summary(fit)

Call:
lm(formula = obs ~ 1)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.58485 -0.14315  0.00559  0.13729  0.66317 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) 0.017019   0.006745   2.523   0.0118 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2133 on 999 degrees of freedom

Note that the estimate of the intercept is significant, although we started the simulation at zero. Let’s look at the residuals, which have the same autocorrelation as the data.

plot(residuals(fit))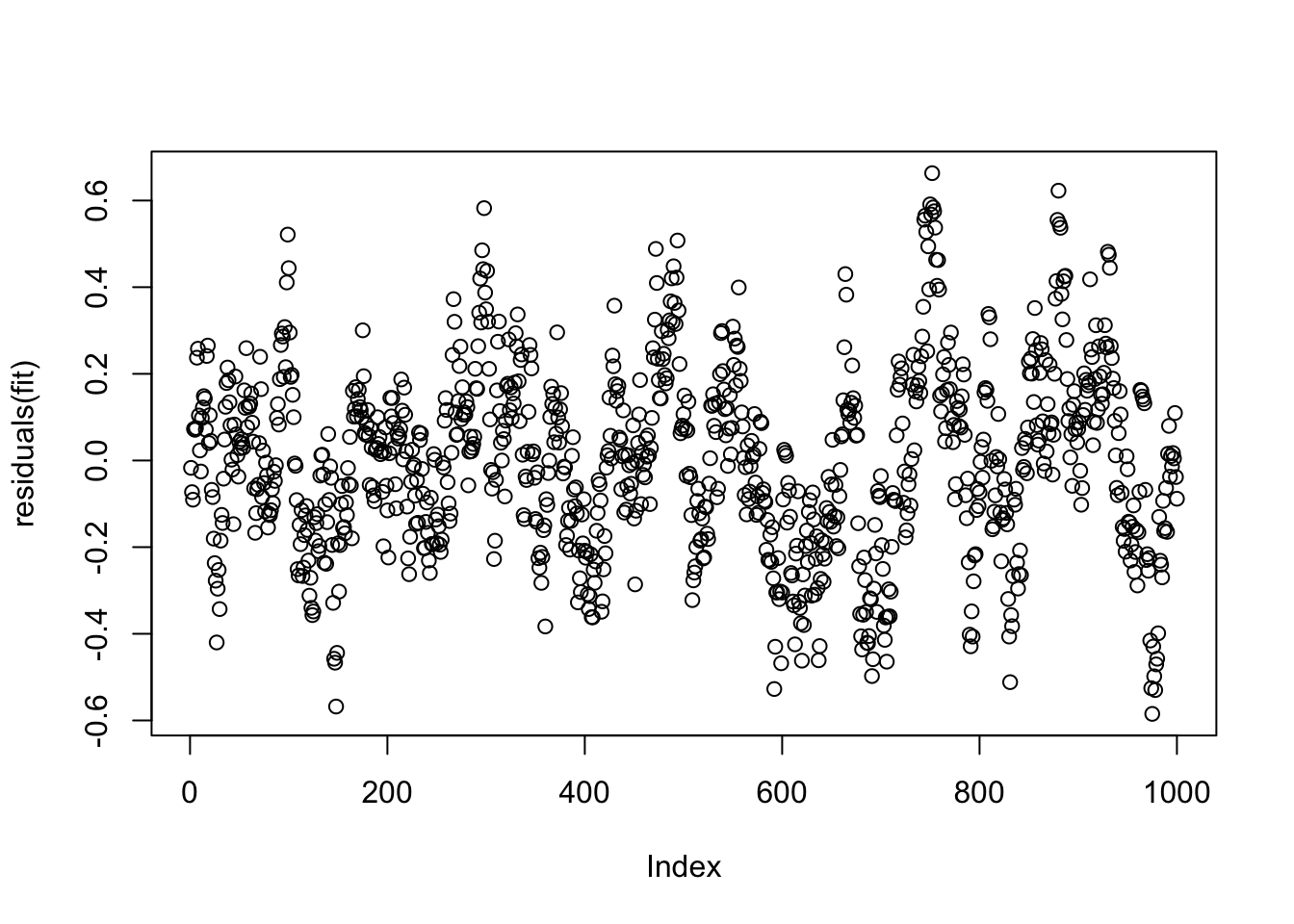

We can quantify the autocorrelation by the acf function, which quantifies correlation between observations as a function of their lag (temporal distance). Note that although we modeled only a lag of 1, we will get correlations with many lags, because the correlation effect “trickles down”.

acf(residuals(fit))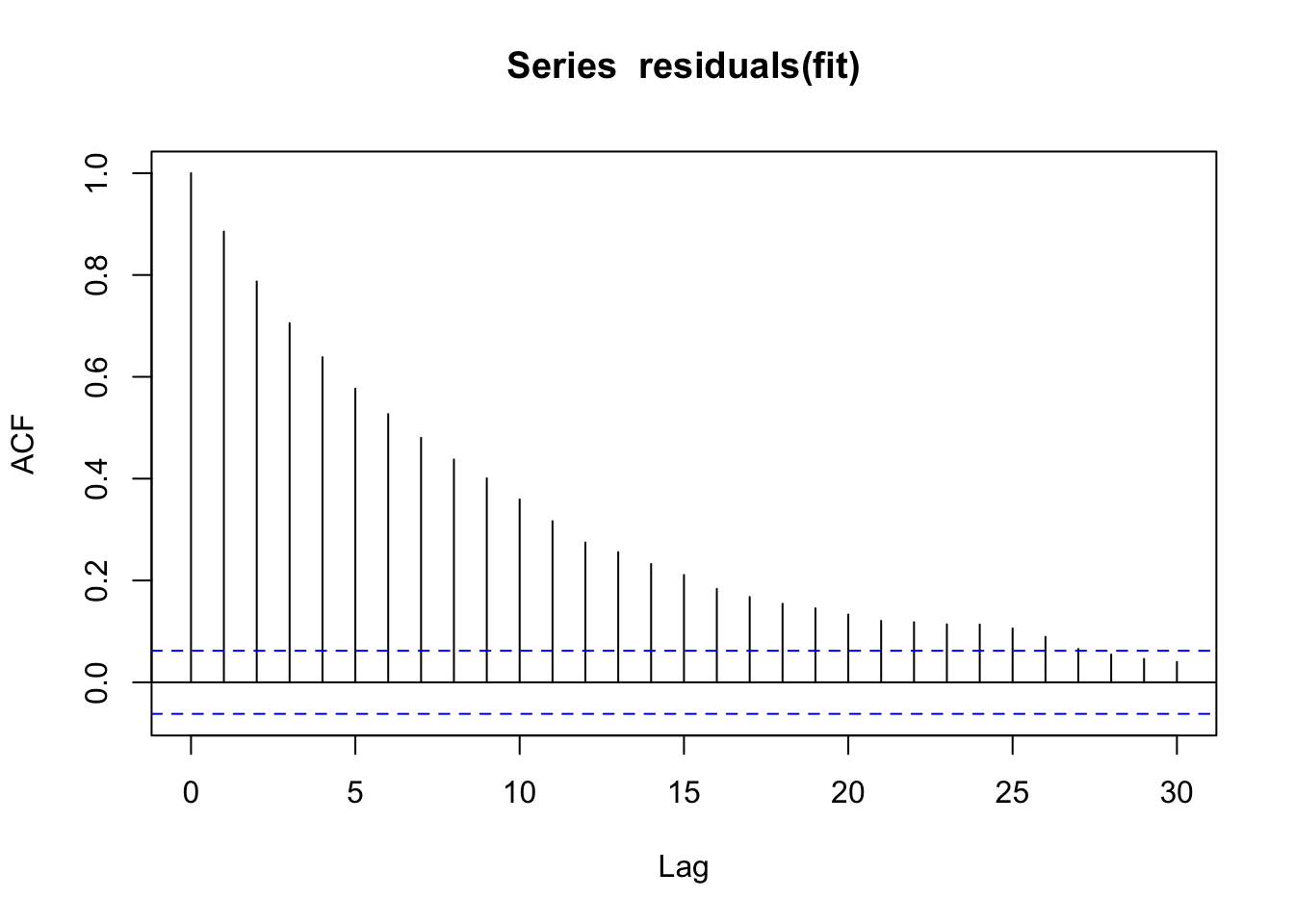

To check what the actual underlying model is, it may be useful to plot the partial correlation coefficient, which is estimated by fitting autoregressive models of successively higher orders and checking their residuals.

pacf(residuals(fit))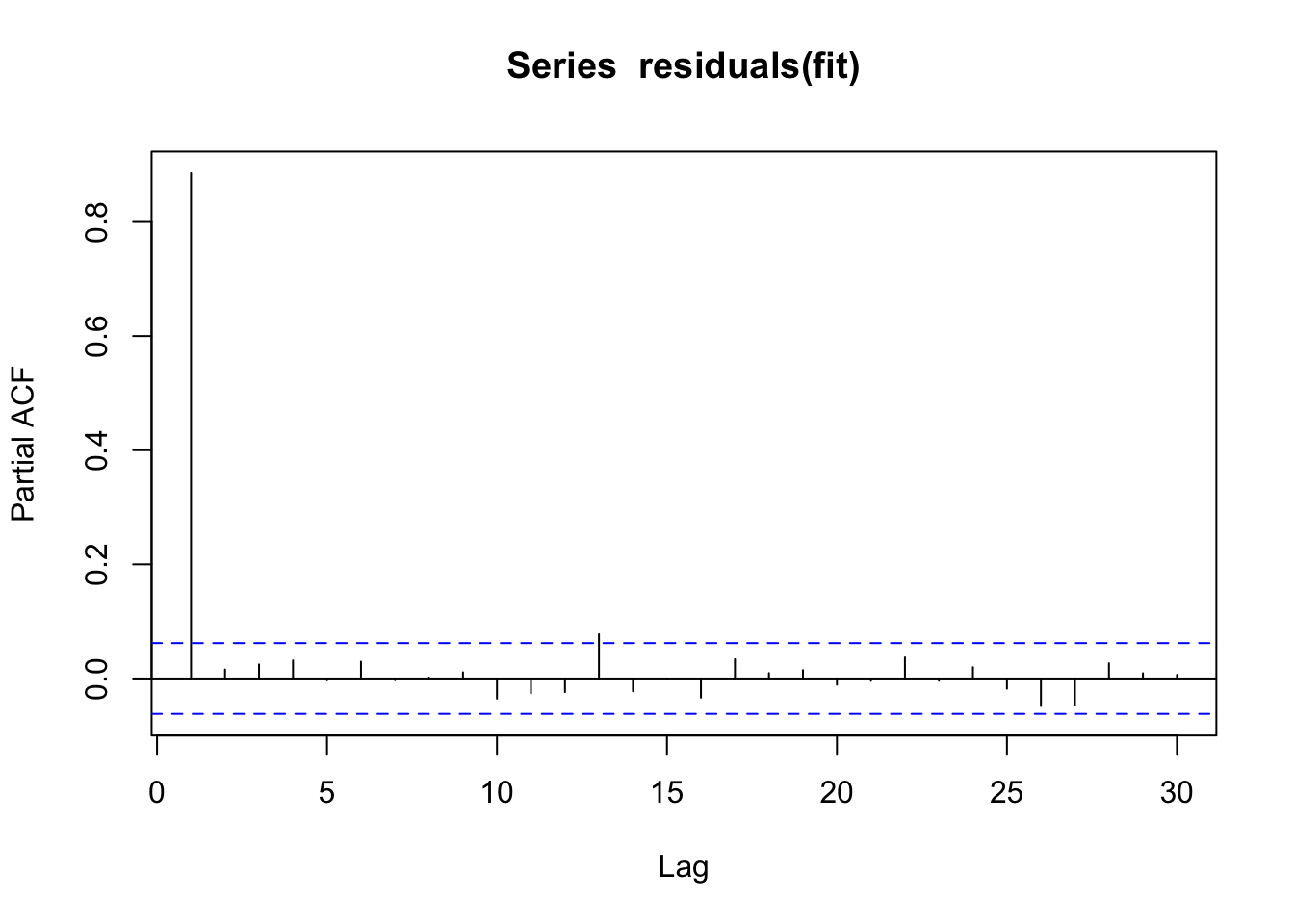

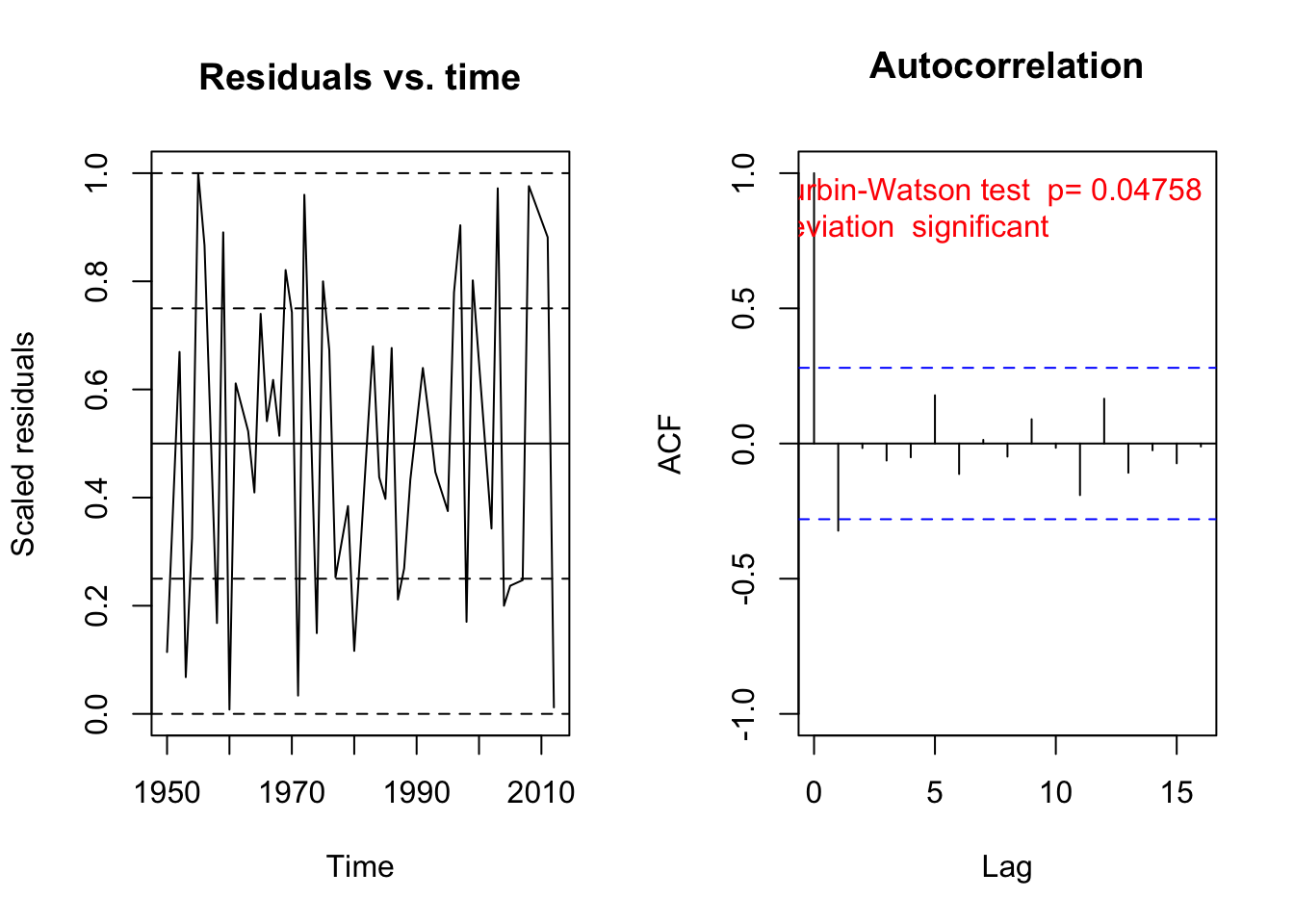
Here, we see that we actually only have a correlation with lag 1. You can also check for temporal correlation with the DHARMa package

library(DHARMa)
This is DHARMa 0.4.7. For overview type '?DHARMa'. For recent changes, type news(package = 'DHARMa')
testTemporalAutocorrelation(fit, time = 1:1000)


    Durbin-Watson test

data:  simulationOutput$scaledResiduals ~ 1
DW = 0.25973, p-value < 2.2e-16
alternative hypothesis: true autocorrelation is not 0
Note

Remember: in general, for spatial / temporal data, there are two processes that can created residual autocorreation:

  1. There is a spatial misfit trend in time / space, which creates a correlation in space / time.
  2. There truly is a spatial correlation, after accounting for the trend.

Unfortunately, the distinction between a larger trend and a correlation is quite fluid. Nevertheless, one should always first check for and remove the trend, typically by including time/space as a predictor, potentially in a flexible way (GAMs come in handy). After this is done, we can fit a model with a temporally/spatially correlated error.

Let’s see how we can fit the AR1 model to data. First, with nlme

library(nlme)

fitGLS = gls(obs~1, corr = corAR1(0.771, form = ~ 1))
summary(fitGLS)
Generalized least squares fit by REML
  Model: obs ~ 1 
  Data: NULL 
        AIC       BIC  logLik
  -1773.104 -1758.384 889.552

Correlation Structure: AR(1)
 Formula: ~1 
 Parameter estimate(s):
      Phi 
0.8865404 

Coefficients:
                 Value  Std.Error   t-value p-value
(Intercept) 0.01620833 0.02741235 0.5912784  0.5545

Standardized residuals:
        Min          Q1         Med          Q3         Max 
-2.72610052 -0.66439347  0.02987808  0.64460052  3.09922846 

Residual standard error: 0.2142402 
Degrees of freedom: 1000 total; 999 residual

Second, with glmmTMB

library(glmmTMB)

time <- factor(1:1000) # time variable
group = factor(rep(1,1000)) # group (for multiple time series)

fitGLMMTMB = glmmTMB(obs ~ ar1(time + 0 | group))
Warning in glmmTMB(obs ~ ar1(time + 0 | group)): use of the 'data' argument is
recommended
summary(fitGLMMTMB)
 Family: gaussian  ( identity )
Formula:          obs ~ ar1(time + 0 | group)

     AIC      BIC   logLik deviance df.resid 
 -1776.7  -1757.1    892.4  -1784.7      996 

Random effects:

Conditional model:
 Groups   Name  Variance  Std.Dev. Corr      
 group    time1 0.0449381 0.21199  0.89 (ar1)
 Residual       0.0002047 0.01431            
Number of obs: 1000, groups:  group, 1

Dispersion estimate for gaussian family (sigma^2): 0.000205 

Conditional model:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)  0.01619    0.02740   0.591    0.555

If you check the results, you can see that

  1. Both models correctly estimate the AR1 parameter
  2. The p-value for the intercept is in both models n.s., as expected
Trend and autocorrelation with glmmTMB

As I mentioned earlier, first detrend and then add correlation structure if there is autocorrelation. After both steps we should no longer see any pattern in the conditional residuals. Unfortunately, checking the conditional residuals is a bit complicated because glmmTMB does not support conditional simulations, while lme4 does, but it does not support correlation structures. However, there is a workaround.

Let’s start with a small simulation with a time trend and autocorrelation:

time = 1:1000/100
y = time +2*(sin(time/0.4)) + rnorm(1000)
data = 
  data.frame(y = y, time = time, timeF = as.factor(1:1000), group = as.factor(1))
plot(y ~time)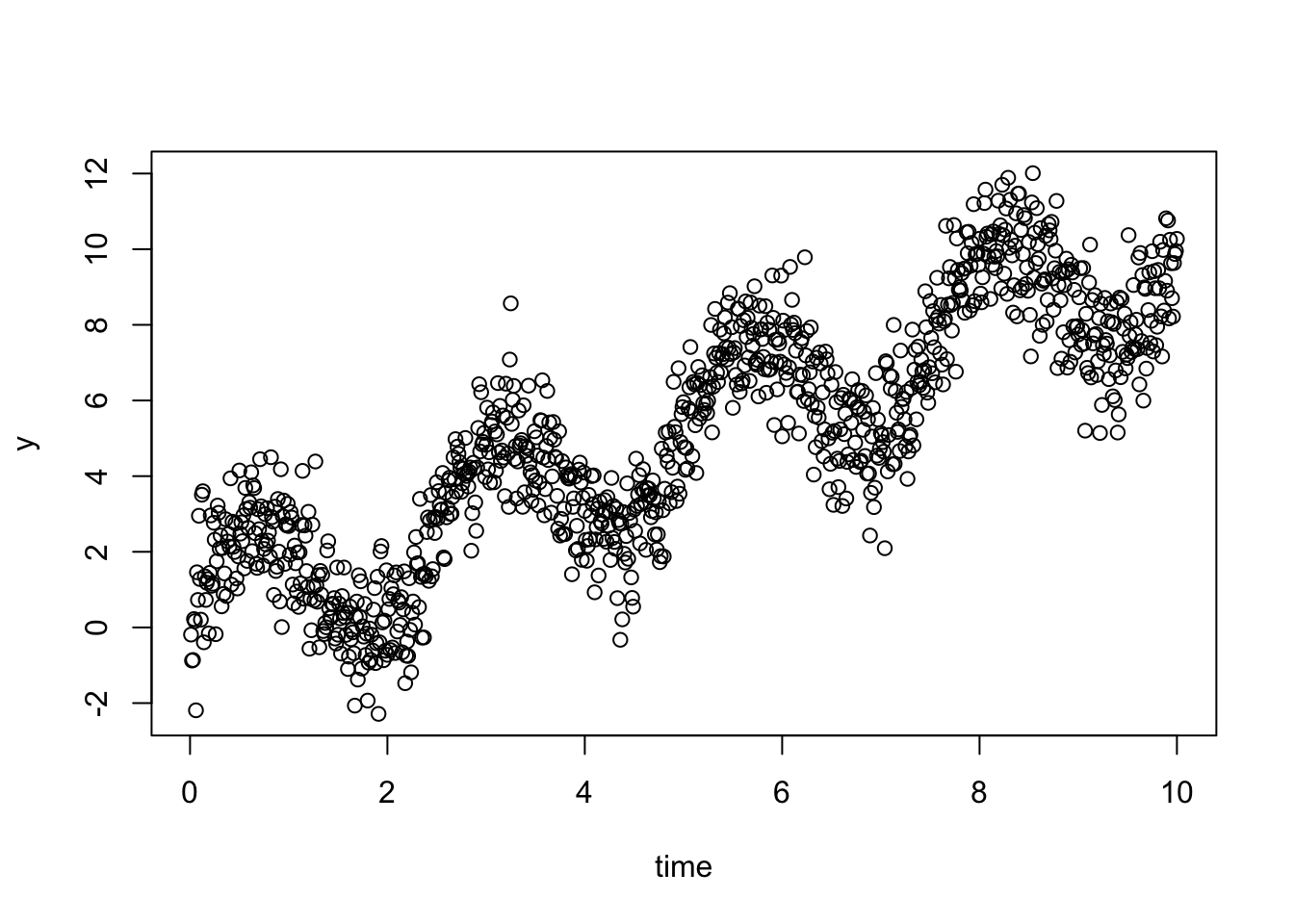

  1. Detrend
fit1 = glmmTMB(y~time, data = data)
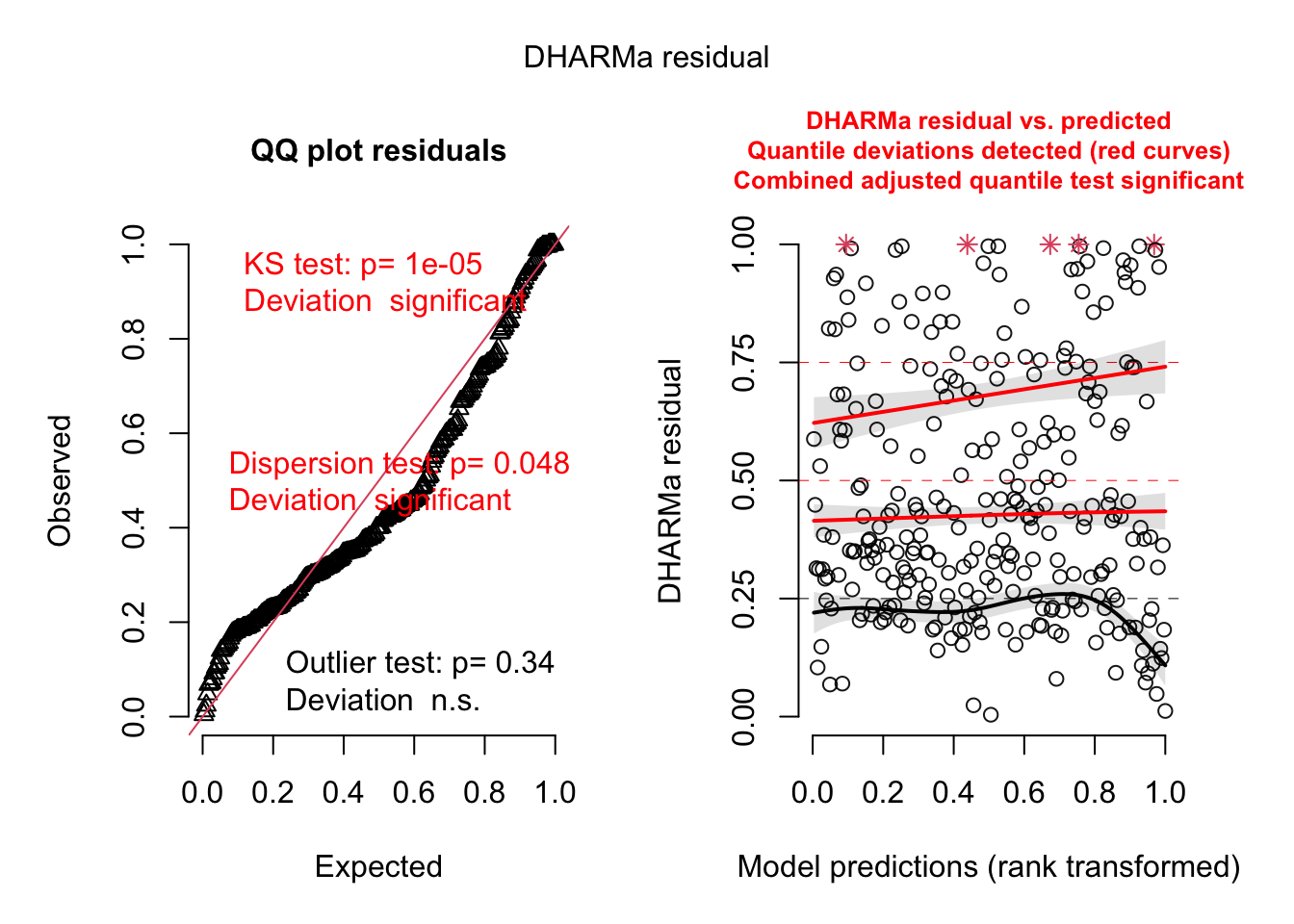
res = simulateResiduals(fit1, plot = TRUE)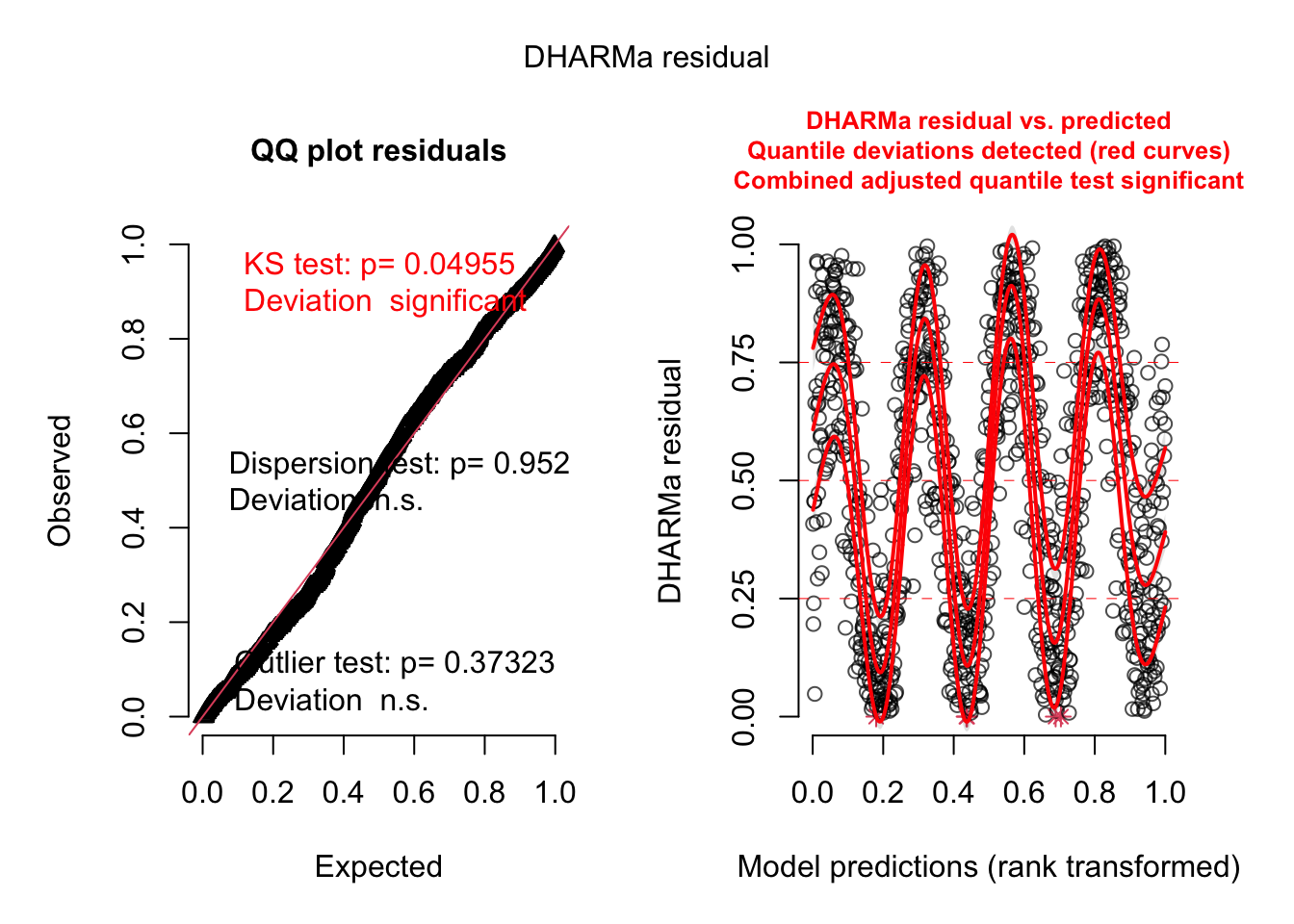

testTemporalAutocorrelation(res, time = data$time)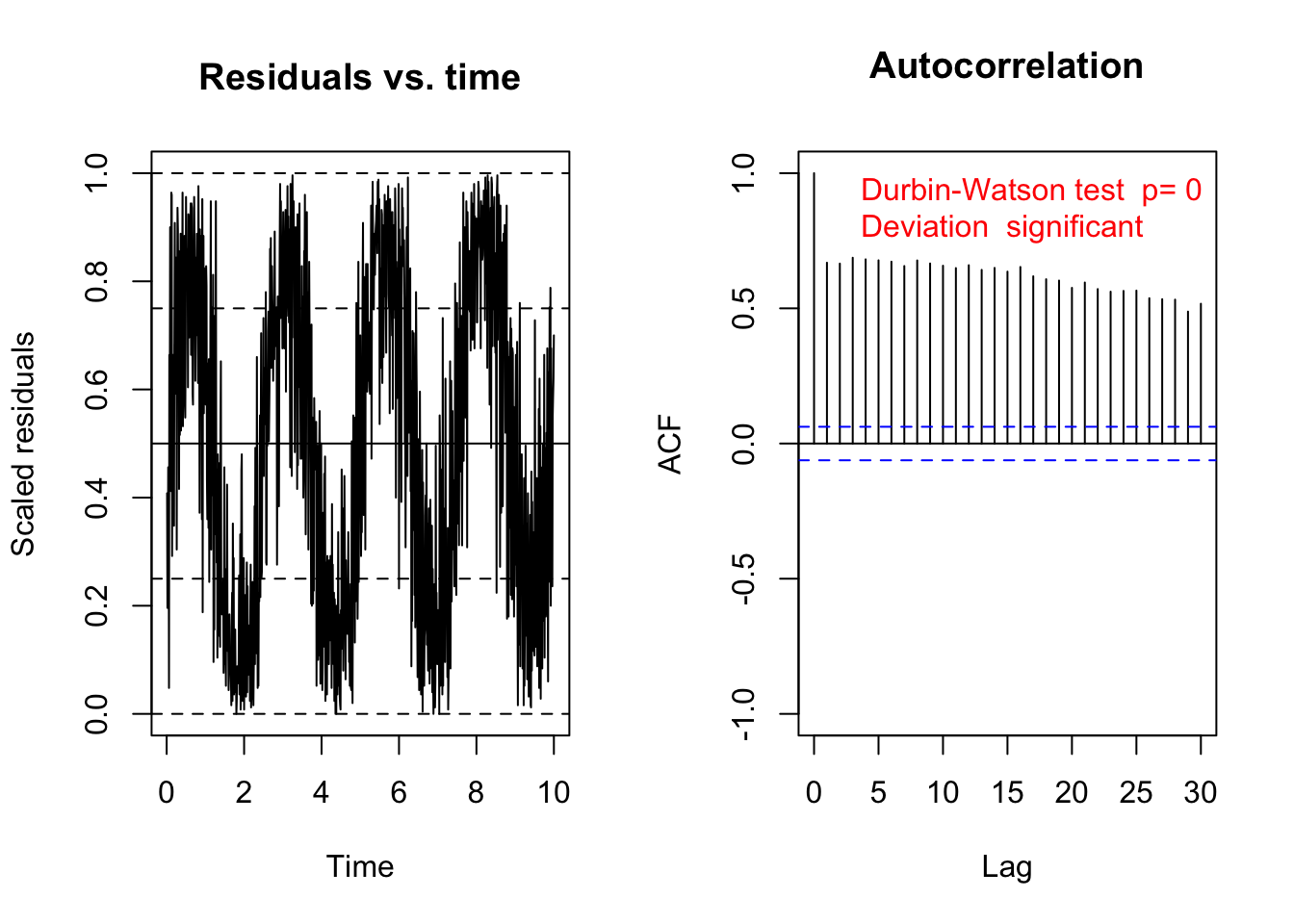


    Durbin-Watson test

data:  simulationOutput$scaledResiduals ~ 1
DW = 0.66181, p-value < 2.2e-16
alternative hypothesis: true autocorrelation is not 0

Test for temporal autocorrelation is siginificant -> add autoregressive structure

  1. Add autoregressive structure
fit2 = glmmTMB(y~time + ar1(0+timeF|group), data = data)
res = simulateResiduals(fit2, plot = TRUE)

The residual plot did not change because glmmTMB:::simulate.glmmTMB does not generate conditional predictions. But we can generate them ourselves:

  1. Create conditional predictions and simulations

We can create a custom DHARMa object with our own simulations:

pred = predict(fit2, re.form = NULL)
simulations = sapply(1:250, function(i) rnorm(1000, pred, summary(fit2)$sigma))
res = createDHARMa(simulations, data$y, pred)
plot(res)

Voila, the residuals look good now!

11.2.1 Exercise - hurricanes revisited?

Excercise

Look at the hurricane study that we used before, which is, after all, temporal data. This data set is located in DHARMa.

library(DHARMa)

fit = glmmTMB(alldeaths ~ scale(MasFem) *
                          (scale(Minpressure_Updated_2014) + scale(NDAM)),
                           data = hurricanes, family = nbinom2)

# Residual checks with DHARMa.
res = simulateResiduals(fit)

# Checking for temporal autocorrelation
res2 = recalculateResiduals(res, group = hurricanes$Year)
testTemporalAutocorrelation(res2, time = unique(hurricanes$Year))


    Durbin-Watson test

data:  simulationOutput$scaledResiduals ~ 1
DW = 2.5518, p-value = 0.04758
alternative hypothesis: true autocorrelation is not 0

We see that there is a tiny bit of autocorrelation. Note that this autocorrelation is negative, so if we have a higher residual in one year, it is lower in the next year. Normally, we would expect temporal autocorrelation to be positive, so this is a bit weird. It could be an effect of people being more careful if there mere many fatalities in the previous year, but it could also be a statistical fluke.

In any case, as an exercise, we want to address the issue - add an AR1 term to the model!

Adding the AR1 to the glmmTMB model

hurricanes$yearF <- factor(hurricanes$Year)
hurricanes$group = factor(rep(1,nrow(hurricanes)))

fit = glmmTMB(alldeaths ~ scale(MasFem) *
                          (scale(Minpressure_Updated_2014) + scale(NDAM))
                          + ar1(yearF + 0 | group),
                           data = hurricanes, family = nbinom2)
Warning in finalizeTMB(TMBStruc, obj, fit, h, data.tmb.old): Model convergence
problem; non-positive-definite Hessian matrix. See vignette('troubleshooting')
summary(fit)
 Family: nbinom2  ( log )
Formula:          
alldeaths ~ scale(MasFem) * (scale(Minpressure_Updated_2014) +  
    scale(NDAM)) + ar1(yearF + 0 | group)
Data: hurricanes

     AIC      BIC   logLik deviance df.resid 
      NA       NA       NA       NA       83 

Random effects:

Conditional model:
 Groups Name      Variance  Std.Dev.  Corr      
 group  yearF1950 1.647e-09 4.058e-05 0.77 (ar1)
Number of obs: 92, groups:  group, 1

Dispersion parameter for nbinom2 family (): 0.787 

Conditional model:
                                              Estimate Std. Error z value
(Intercept)                                     2.5034     0.1231  20.341
scale(MasFem)                                   0.1237     0.1210   1.022
scale(Minpressure_Updated_2014)                -0.5425     0.1603  -3.384
scale(NDAM)                                     0.8988     0.2190   4.105
scale(MasFem):scale(Minpressure_Updated_2014)   0.3758     0.1731   2.171
scale(MasFem):scale(NDAM)                       0.6629     0.1999   3.316
                                              Pr(>|z|)    
(Intercept)                                    < 2e-16 ***
scale(MasFem)                                 0.306925    
scale(Minpressure_Updated_2014)               0.000715 ***
scale(NDAM)                                   4.05e-05 ***
scale(MasFem):scale(Minpressure_Updated_2014) 0.029903 *  
scale(MasFem):scale(NDAM)                     0.000915 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Careful, we are getting a convergence warning here! You should take these warnings seriously! If we look at the fitted values, we see that we estimate positive temporal autocorrelation, although the plots showed negative autocorrelation. Let’s fit a reduced model:

fit = glmmTMB(alldeaths ~ scale(MasFem) 
                          + ar1(yearF + 0 | group),
                           data = hurricanes, family = nbinom2)
summary(fit)
 Family: nbinom2  ( log )
Formula:          alldeaths ~ scale(MasFem) + ar1(yearF + 0 | group)
Data: hurricanes

     AIC      BIC   logLik deviance df.resid 
   707.6    720.3   -348.8    697.6       87 

Random effects:

Conditional model:
 Groups Name      Variance Std.Dev. Corr       
 group  yearF1950 0.7204   0.8487   -0.24 (ar1)
Number of obs: 92, groups:  group, 1

Dispersion parameter for nbinom2 family (): 0.592 

Conditional model:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept)     2.7335     0.2128   12.85   <2e-16 ***
scale(MasFem)   0.1351     0.1850    0.73    0.465    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Now we get the right estimates for the autocorrelation, but of course this is not the model we want. You should now go to the optimizer settings and see if you can fix this. If you can’t fix it, you could maybe

11.3 Spatial Correlation Structures

Spatial models work very similar to the temporal models. This time, we start directly with an example, using a data set with the thickness of coal seams, that we try to predict with a spatial (soil) predictor.

library(EcoData)
plot(thick ~ soil, data = thickness)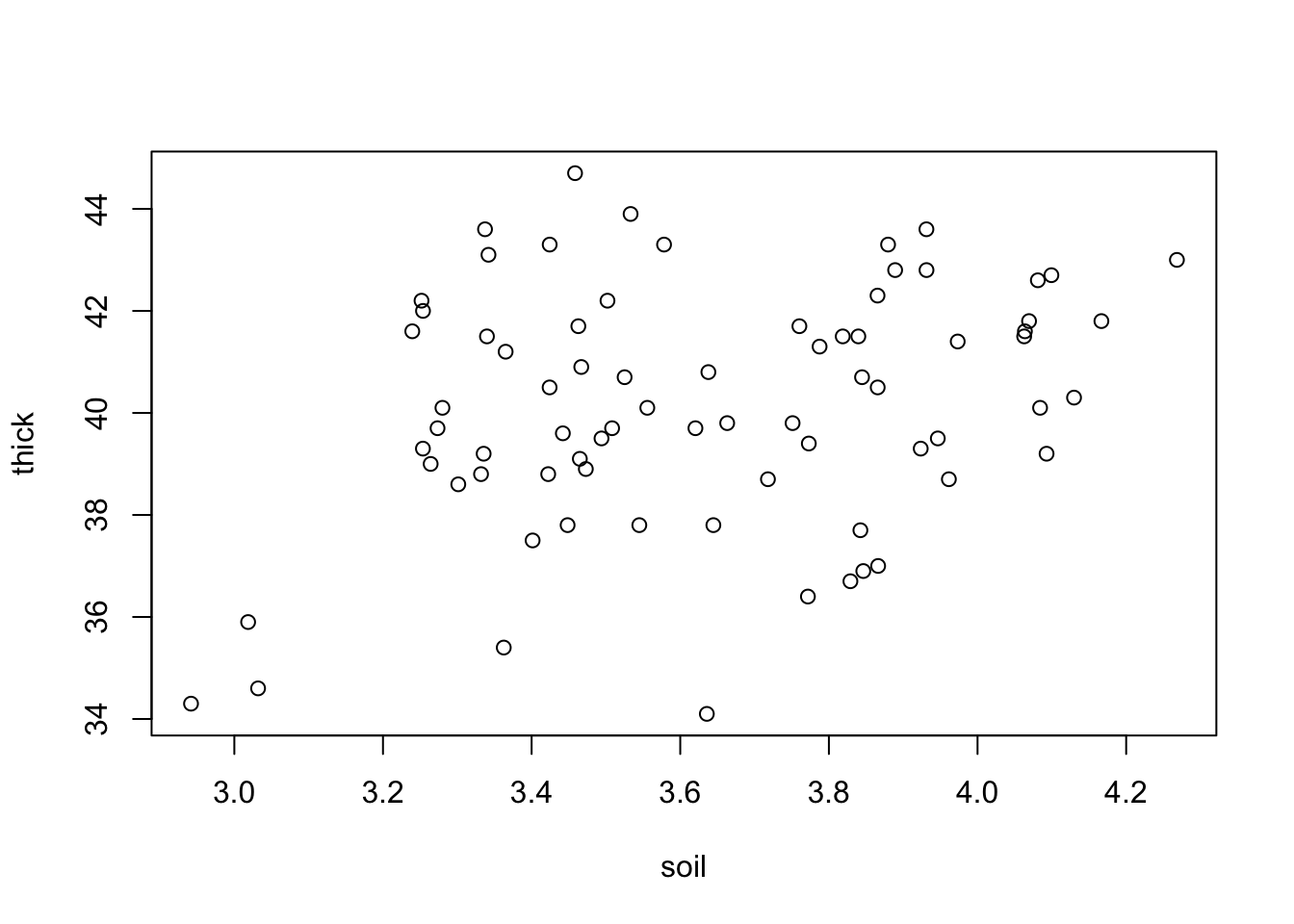

Let’s fit a simple LM to this

fit = lm(thick ~ soil, data = thickness)
summary(fit)

Call:
lm(formula = thick ~ soil, data = thickness)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.0414 -1.1975  0.0876  1.4836  4.9584 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  31.9420     3.1570  10.118 1.54e-15 ***
soil          2.2552     0.8656   2.605   0.0111 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.278 on 73 degrees of freedom
Multiple R-squared:  0.08508,   Adjusted R-squared:  0.07254 
F-statistic: 6.788 on 1 and 73 DF,  p-value: 0.01111

DHARMa checks:

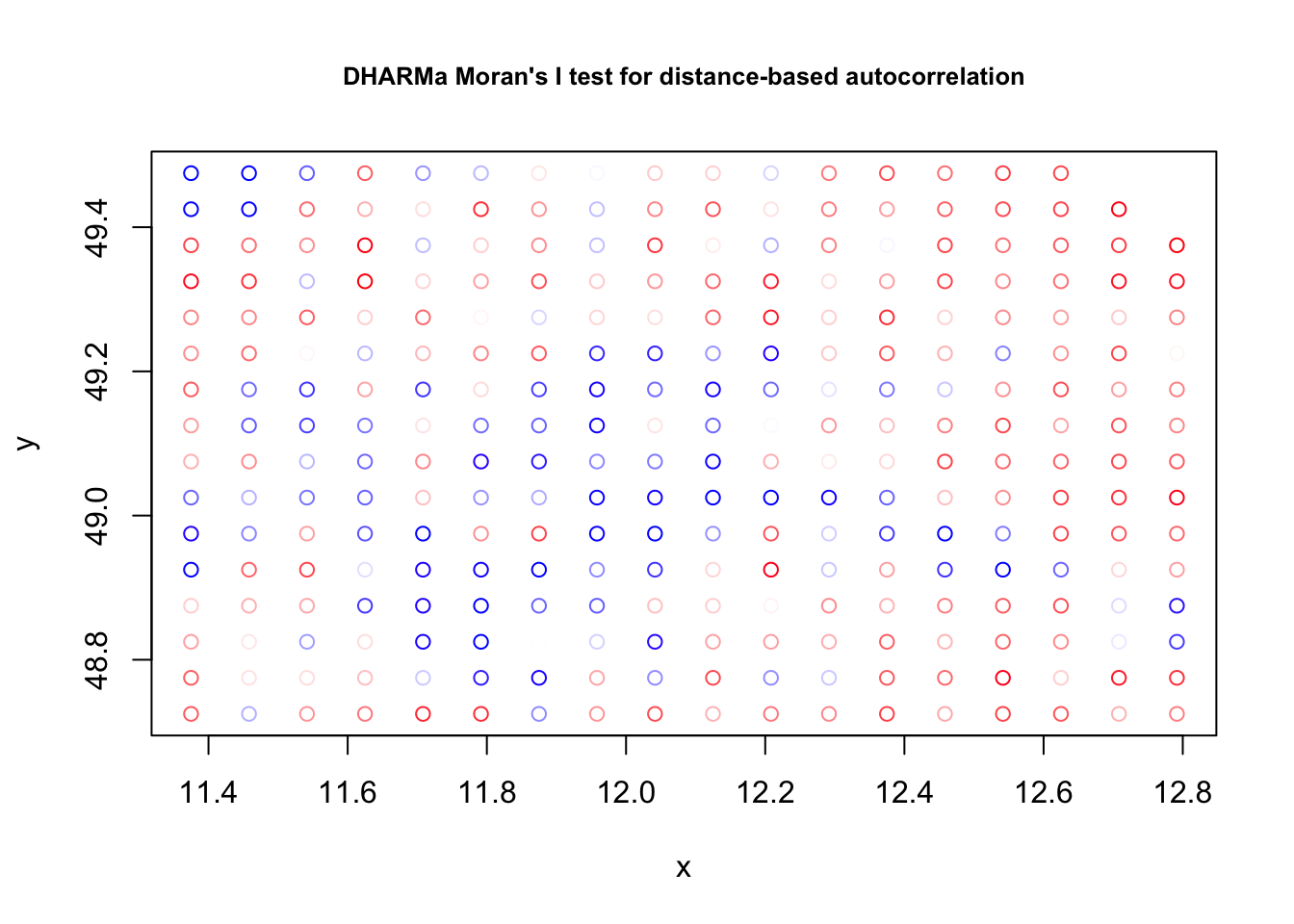
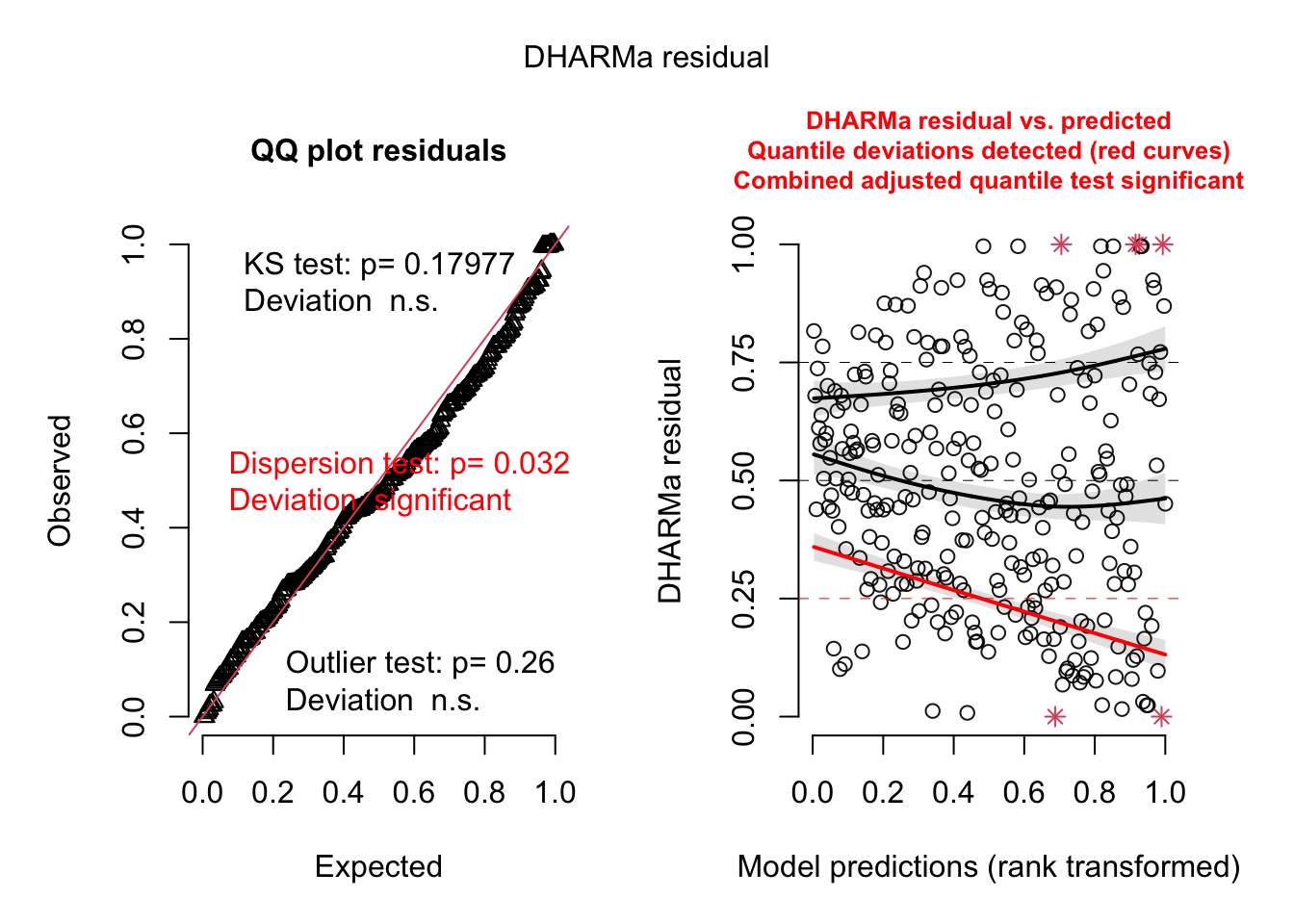
res = simulateResiduals(fit)
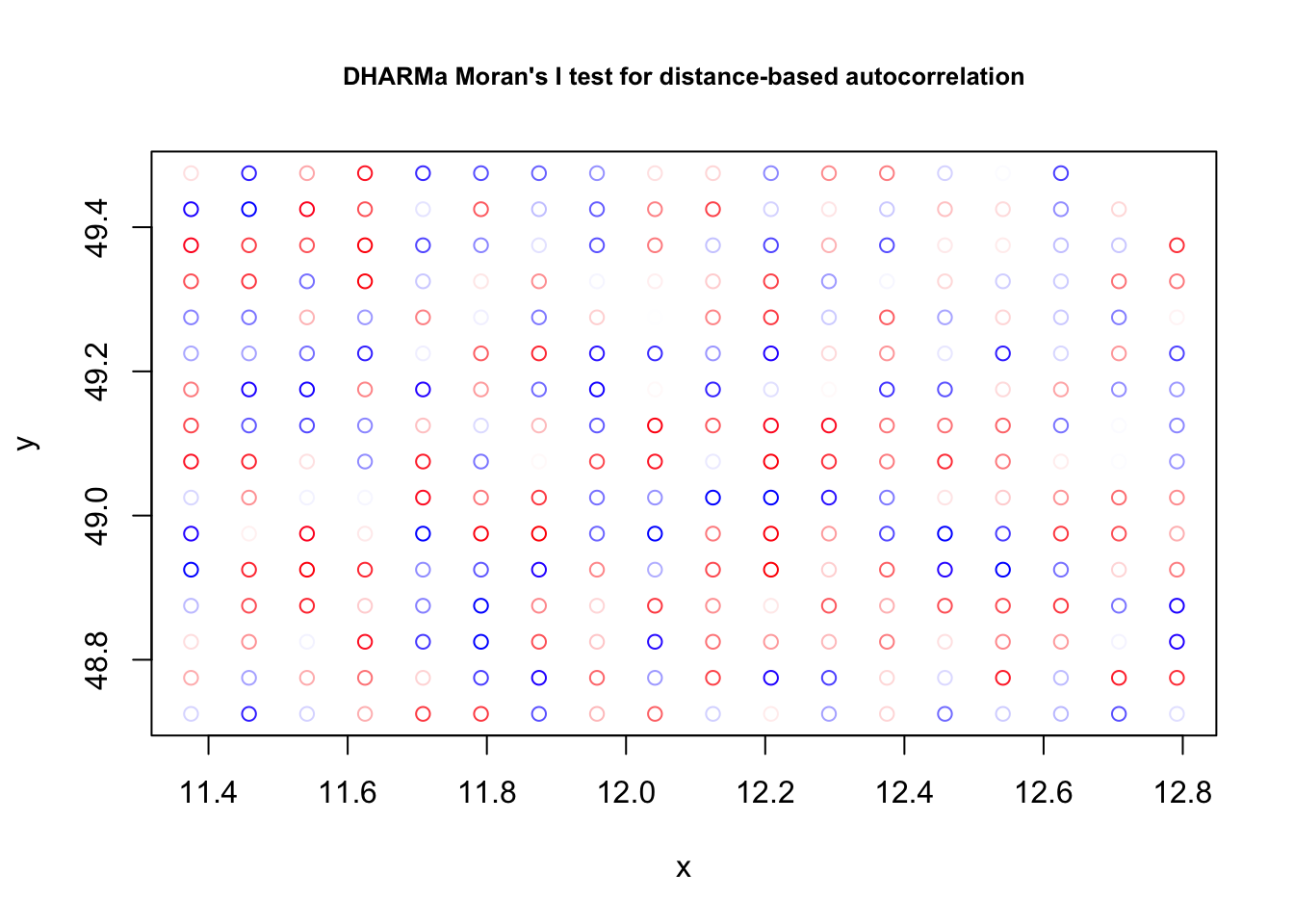
testSpatialAutocorrelation(res, x = thickness$north, y = thickness$east)


    DHARMa Moran's I test for distance-based autocorrelation

data:  res
observed = 0.210870, expected = -0.013514, sd = 0.021940, p-value <
2.2e-16
alternative hypothesis: Distance-based autocorrelation

For spatial data, we often look at spatial variograms, which are similar to an acf but in spatial directions

library(gstat)
tann.dir.vgm = variogram(residuals(fit) ~ 1,
                         loc =~ east + north, data = thickness,
                         alpha = c(0, 45, 90, 135))
plot(tann.dir.vgm)

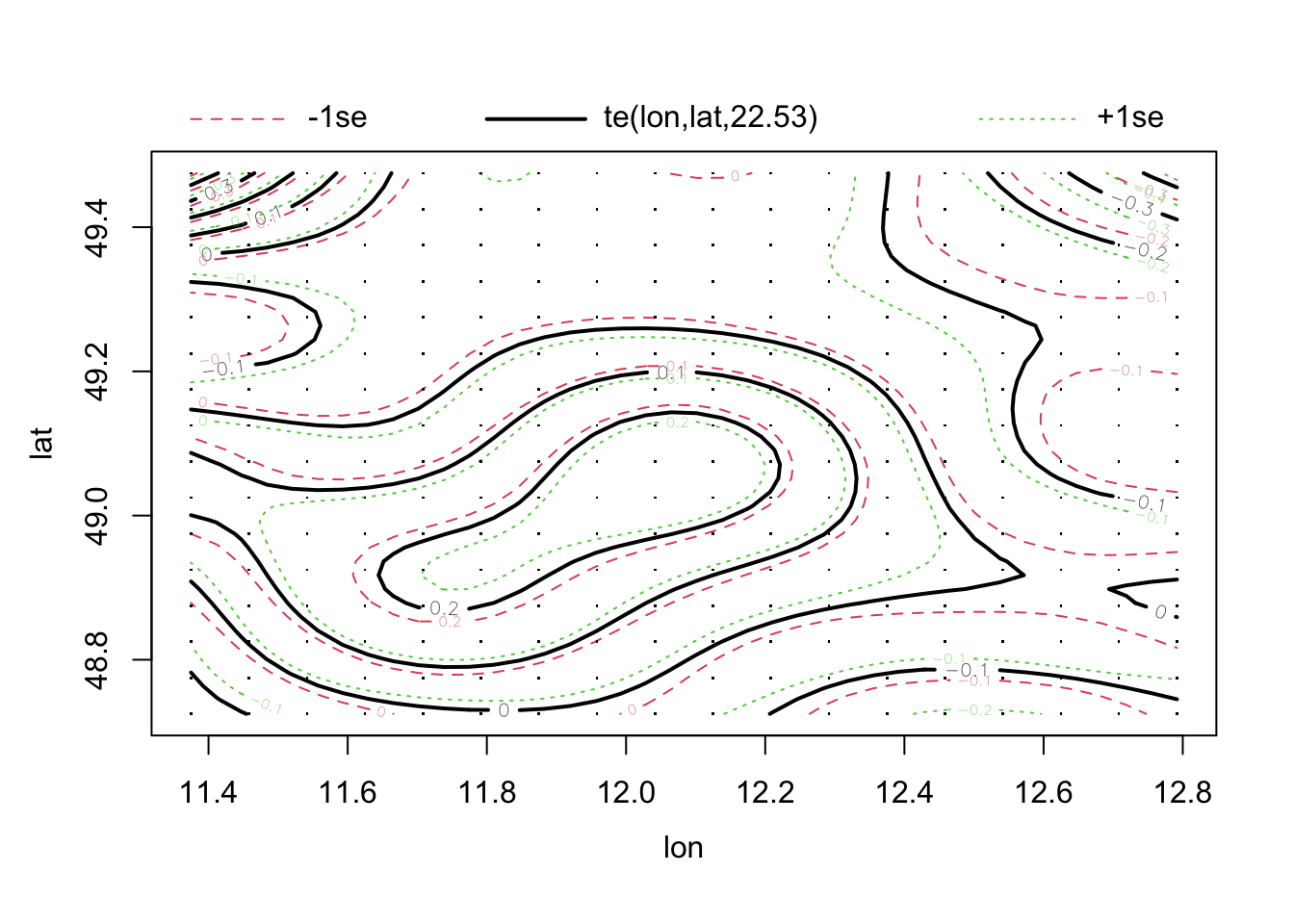
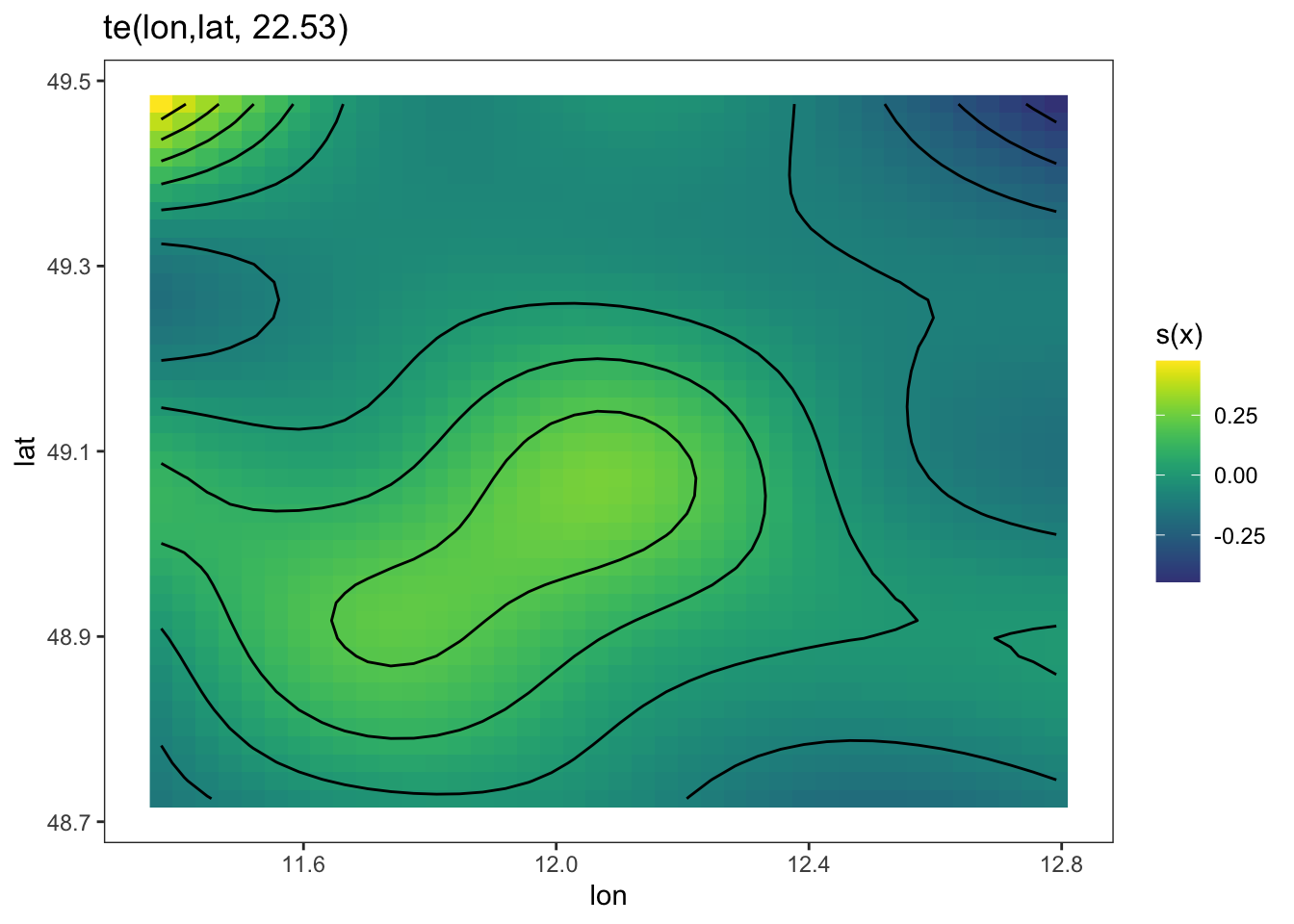
Both the DHARMa plots and the variograms are more indicative of a spatial trend. Let’s remove this with a 2d-spine, called a tensor spline:

library(mgcv)

fit1 = gam(thick ~ soil + te(east, north) , data = thickness)
summary(fit1)

Family: gaussian 
Link function: identity 

Formula:
thick ~ soil + te(east, north)

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 39.68933    0.26498 149.780   <2e-16 ***
soil         0.12363    0.07275   1.699   0.0952 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
                 edf Ref.df     F p-value    
te(east,north) 21.09  22.77 721.3  <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.996   Deviance explained = 99.7%
GCV = 0.033201  Scale est. = 0.022981  n = 75
plot(fit1, pages = 0, lwd = 2)

We can check the model again, and the problem is gone

res = simulateResiduals(fit1)
Registered S3 method overwritten by 'GGally':
  method from   
  +.gg   ggplot2
Registered S3 method overwritten by 'mgcViz':
  method from  
  +.gg   GGally
testSpatialAutocorrelation(res, x = thickness$north, y = thickness$east)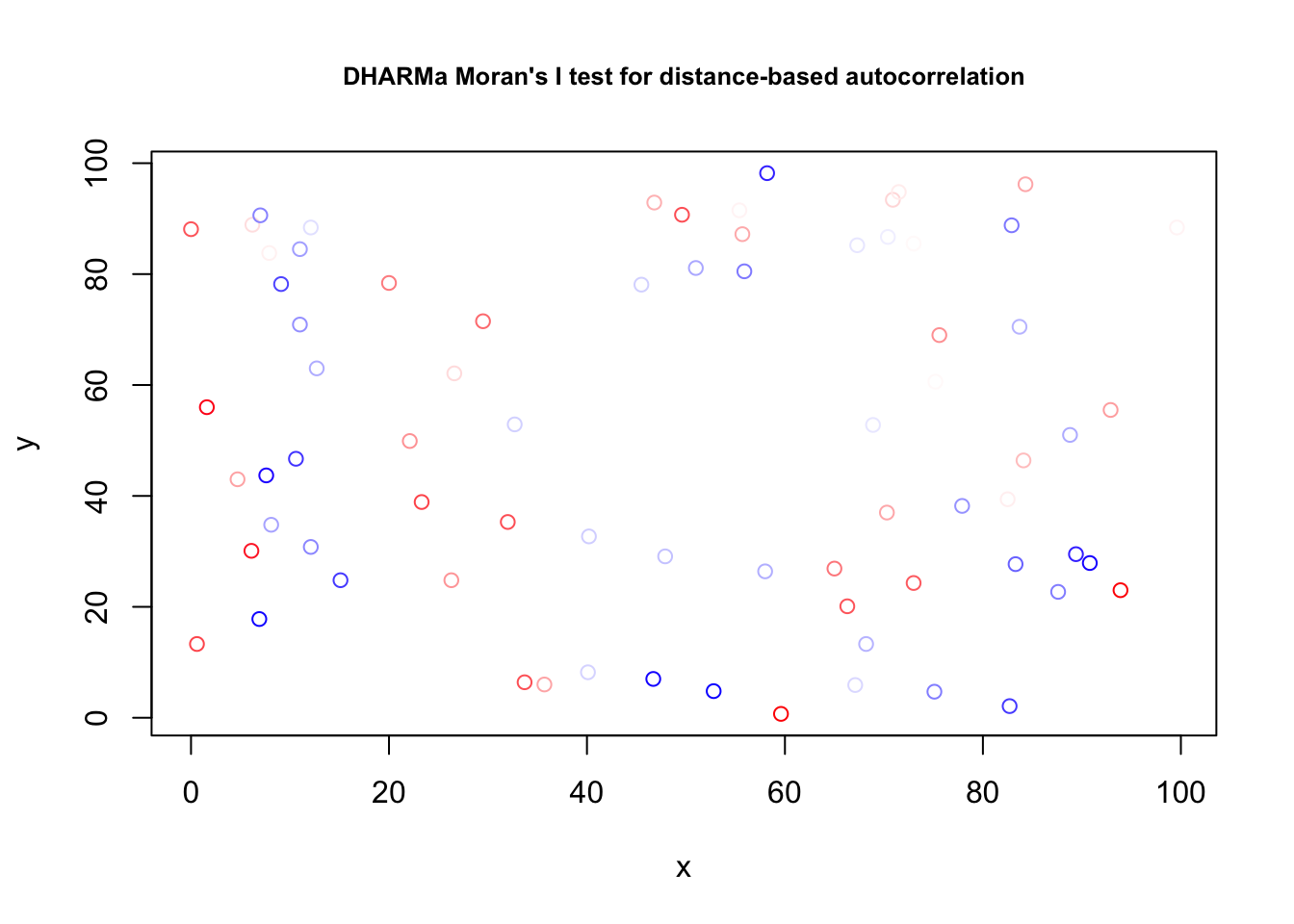


    DHARMa Moran's I test for distance-based autocorrelation

data:  res
observed = -0.024242, expected = -0.013514, sd = 0.021860, p-value =
0.6236
alternative hypothesis: Distance-based autocorrelation

Almost the same, but simpler:

fit = lm(thick ~ soil + north + I(north^2), data = thickness)

If we would have still seen a signal, we should have fit an autoregressive model. Here it’s not necessary, but just to show you the syntax - first nlme:

fit2 = gls(thick ~ soil , correlation = corExp(form =~ east + north) , data = thickness)
summary(fit2)
Generalized least squares fit by REML
  Model: thick ~ soil 
  Data: thickness 
       AIC      BIC    logLik
  164.3474 173.5092 -78.17368

Correlation Structure: Exponential spatial correlation
 Formula: ~east + north 
 Parameter estimate(s):
   range 
719.4122 

Coefficients:
               Value Std.Error  t-value p-value
(Intercept) 42.81488  5.314542 8.056176  0.0000
soil         0.02662  0.199737 0.133289  0.8943

 Correlation: 
     (Intr)
soil -0.12 

Standardized residuals:
       Min         Q1        Med         Q3        Max 
-1.5811122 -0.7276873 -0.5028102 -0.2092991  0.3217326 

Residual standard error: 5.573088 
Degrees of freedom: 75 total; 73 residual

Second, for glmmTMB. Here, we again have to prepare the data first

thickness$pos <- numFactor(thickness$east, 
                           thickness$north)
thickness$group <- factor(rep(1, nrow(thickness)))

fit3 = glmmTMB(thick ~ soil + exp(pos + 0 | group) , data = thickness)

The output of summary is a bit chunky, which is why I suppress it here

summary(fit3)

If you wonder why there is such a large correlation matrix displayed: both the AR1 and the exp(pos + 0 | group) structure impose a particular correlation structure on the random effects. Per default, glmmTMB shows correlations of random effects if they are estimated. In the case of the AR1 structure, the programmers apparently surpressed this, and just showed the stimate of the AR1 parameter. Here, however, they didn’t implement this feature, so you see the entire correlation structure, which is, admittedly, less helpful and should be changed.

11.3.1 Exercise - does agriculture influence plant species richness?

Plant counts in Regensburg

Use the dataset EcoData::plantcounts. Our scientific question is if richness ~ agrarea. Help on the dataset, as well as a few initial plots, is in the help of ?plantcounts.

This is count data, so start with a Poisson or Neg Binom GLM. The quadrats are not all equally sized, so you should include an offest to account for area. Then, check for spatial autocorrelation.

If you find autocorrelation that cannot be removed with a gam, the problem is that the gls function that we have used so far only extends lm, and not glm models. In this case, you can either read up in https://cran.r-project.org/web/packages/glmmTMB/vignettes/covstruct.html how to specify a spatial covariance in glmmTMB, or just log transform your counts + 1, and fit a gls.

?EcoData::plantcounts

plants_sf <- plantcounts
str(plants_sf)
'data.frame':   285 obs. of  6 variables:
 $ tk      : int  65341 65342 65343 65344 65351 65352 65353 65354 65361 65362 ...
 $ area    : num  33.6 33.6 33.6 33.6 33.6 ...
 $ richness: int  767 770 741 756 550 434 433 448 527 505 ...
 $ agrarea : num  0.488 0.431 0.484 0.598 0.422 ...
 $ lon     : num  11.4 11.5 11.4 11.5 11.5 ...
 $ lat     : num  49.5 49.5 49.4 49.4 49.5 ...
plants_sf$agrarea_scaled <- scale(plants_sf$agrarea)

plants_sf$longitude <- plants_sf$lon
plants_sf$latitude <- plants_sf$lat
library(sf)
plants_sf <- sf::st_as_sf(plants_sf, coords = c('longitude', 'latitude'), crs
                          = st_crs("+proj=longlat +ellps=bessel
                                   +towgs84=606,23,413,0,0,0,0 +no_defs"))

library(mapview)
mapview(plants_sf["richness"], map.types = "OpenTopoMap")
fit <-  glmmTMB::glmmTMB(richness ~ agrarea_scaled + offset(log(area)),
                family = nbinom1, data = plants_sf)
summary(fit)
 Family: nbinom1  ( log )
Formula:          richness ~ agrarea_scaled + offset(log(area))
Data: plants_sf

     AIC      BIC   logLik deviance df.resid 
  3348.8   3359.8  -1671.4   3342.8      282 


Dispersion parameter for nbinom1 family (): 14.3 

Conditional model:
               Estimate Std. Error z value Pr(>|z|)    
(Intercept)     2.66825    0.01047  254.79  < 2e-16 ***
agrarea_scaled -0.03316    0.01021   -3.25  0.00117 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
library(DHARMa)
res <- simulateResiduals(fit)
plot(res)

testSpatialAutocorrelation(res, x = plants_sf$lon, y =  plants_sf$lat)


    DHARMa Moran's I test for distance-based autocorrelation

data:  res
observed = 0.0958792, expected = -0.0035211, sd = 0.0047788, p-value <
2.2e-16
alternative hypothesis: Distance-based autocorrelation
fit2<-mgcv::gam(richness ~ agrarea_scaled + te(lon, lat),
            offset(log(area)), family = nb, data = plants_sf)
summary(fit2)

Family: Negative Binomial(67.736) 
Link function: log 

Formula:
richness ~ agrarea_scaled + te(lon, lat)

Parametric coefficients:
                Estimate Std. Error z value Pr(>|z|)    
(Intercept)     6.183373   0.004096 1509.72  < 2e-16 ***
agrarea_scaled -0.024366   0.005355   -4.55 5.37e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
              edf Ref.df Chi.sq p-value    
te(lon,lat) 22.53  23.76  850.3  <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.413   Deviance explained = 50.2%
-REML = 5622.6  Scale est. = 1         n = 285
plot(fit2)

library(mgcViz)
b <- getViz(fit2)
print(plot(b, allTerms = F), pages = 1) # Calls print.plotGam()

#plotRGL(sm(b, 1), residuals = TRUE)

res <- simulateResiduals(fit2)
plot(res)

testSpatialAutocorrelation(res, x = plants_sf$lon, y =  plants_sf$lat)


    DHARMa Moran's I test for distance-based autocorrelation

data:  res
observed = -0.0030357, expected = -0.0035211, sd = 0.0047800, p-value =
0.9191
alternative hypothesis: Distance-based autocorrelation

11.4 Phylogenetic Structures (PGLS)

This is mostly taken from https://lukejharmon.github.io/ilhabela/instruction/2015/07/03/PGLS/. The two datasets associated with this example are in the EcoData package.

Perform analysis:

library(EcoData)
library(ape)
library(geiger)
library(nlme)
library(phytools)
library(DHARMa)

To plot the phylogenetic tree, use

plot(anolisTree)

Regress species traits

# Check whether names are matching in both files.
name.check(anolisTree, anolisData)
$tree_not_data
  [1] "ahli"            "alayoni"         "alfaroi"         "aliniger"       
  [5] "allisoni"        "allogus"         "altitudinalis"   "alumina"        
  [9] "alutaceus"       "angusticeps"     "argenteolus"     "argillaceus"    
 [13] "armouri"         "bahorucoensis"   "baleatus"        "baracoae"       
 [17] "barahonae"       "barbatus"        "barbouri"        "bartschi"       
 [21] "bremeri"         "breslini"        "brevirostris"    "caudalis"       
 [25] "centralis"       "chamaeleonides"  "chlorocyanus"    "christophei"    
 [29] "clivicola"       "coelestinus"     "confusus"        "cooki"          
 [33] "cristatellus"    "cupeyalensis"    "cuvieri"         "cyanopleurus"   
 [37] "cybotes"         "darlingtoni"     "distichus"       "dolichocephalus"
 [41] "equestris"       "etheridgei"      "eugenegrahami"   "evermanni"      
 [45] "fowleri"         "garmani"         "grahami"         "guafe"          
 [49] "guamuhaya"       "guazuma"         "gundlachi"       "haetianus"      
 [53] "hendersoni"      "homolechis"      "imias"           "inexpectatus"   
 [57] "insolitus"       "isolepis"        "jubar"           "krugi"          
 [61] "lineatopus"      "longitibialis"   "loysiana"        "lucius"         
 [65] "luteogularis"    "macilentus"      "marcanoi"        "marron"         
 [69] "mestrei"         "monticola"       "noblei"          "occultus"       
 [73] "olssoni"         "opalinus"        "ophiolepis"      "oporinus"       
 [77] "paternus"        "placidus"        "poncensis"       "porcatus"       
 [81] "porcus"          "pulchellus"      "pumilis"         "quadriocellifer"
 [85] "reconditus"      "ricordii"        "rubribarbus"     "sagrei"         
 [89] "semilineatus"    "sheplani"        "shrevei"         "singularis"     
 [93] "smallwoodi"      "strahmi"         "stratulus"       "valencienni"    
 [97] "vanidicus"       "vermiculatus"    "websteri"        "whitemani"      

$data_not_tree
  [1] "1"   "10"  "100" "11"  "12"  "13"  "14"  "15"  "16"  "17"  "18"  "19" 
 [13] "2"   "20"  "21"  "22"  "23"  "24"  "25"  "26"  "27"  "28"  "29"  "3"  
 [25] "30"  "31"  "32"  "33"  "34"  "35"  "36"  "37"  "38"  "39"  "4"   "40" 
 [37] "41"  "42"  "43"  "44"  "45"  "46"  "47"  "48"  "49"  "5"   "50"  "51" 
 [49] "52"  "53"  "54"  "55"  "56"  "57"  "58"  "59"  "6"   "60"  "61"  "62" 
 [61] "63"  "64"  "65"  "66"  "67"  "68"  "69"  "7"   "70"  "71"  "72"  "73" 
 [73] "74"  "75"  "76"  "77"  "78"  "79"  "8"   "80"  "81"  "82"  "83"  "84" 
 [85] "85"  "86"  "87"  "88"  "89"  "9"   "90"  "91"  "92"  "93"  "94"  "95" 
 [97] "96"  "97"  "98"  "99" 
# Plot traits.
plot(anolisData[, c("awesomeness", "hostility")])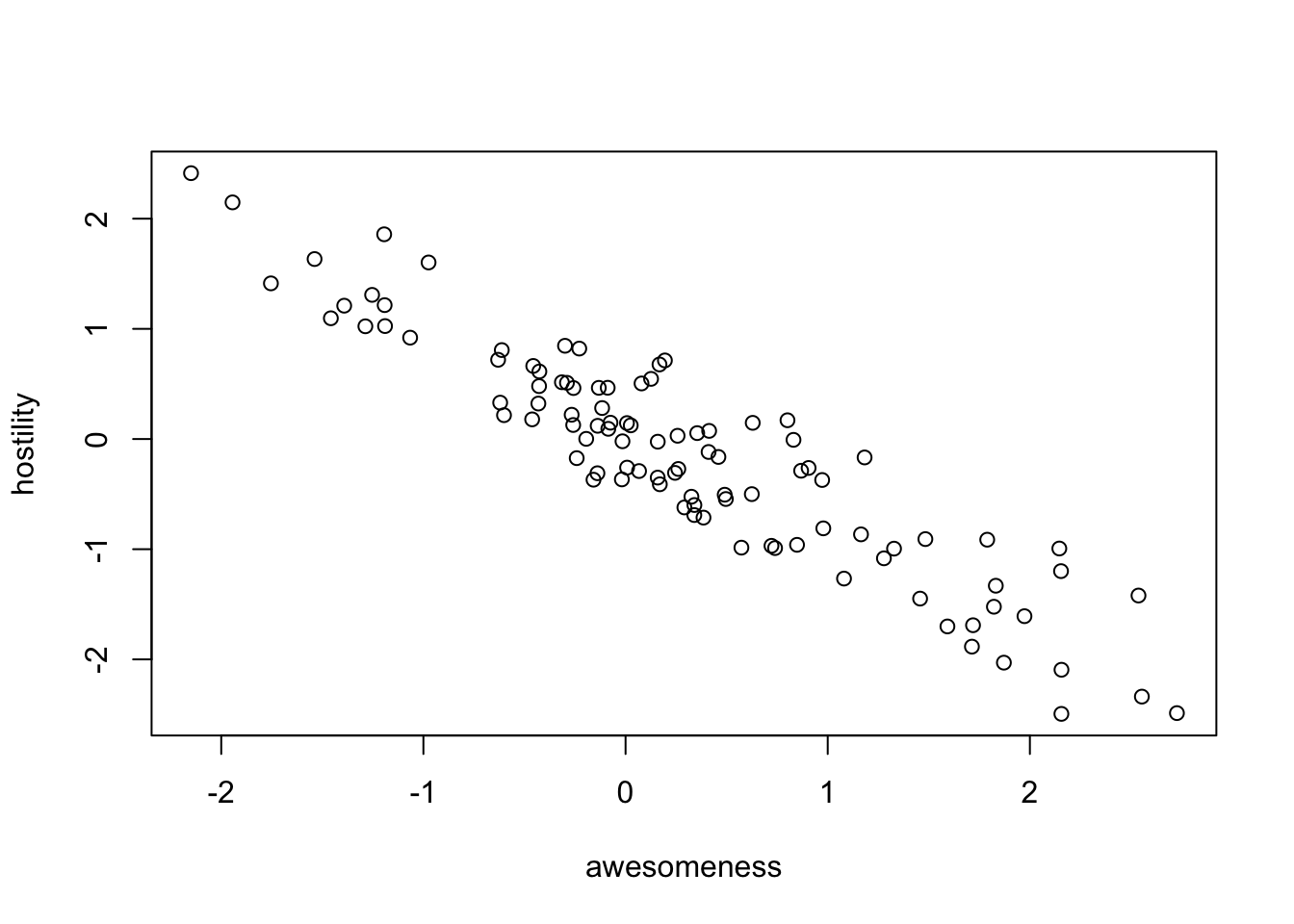

plot(hostility ~ awesomeness, data = anolisData)
fit = lm(hostility ~ awesomeness, data = anolisData)
summary(fit)

Call:
lm(formula = hostility ~ awesomeness, data = anolisData)

Residuals:
    Min      1Q  Median      3Q     Max 
-0.7035 -0.3065 -0.0416  0.2440  0.7884 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.10843    0.03953   2.743  0.00724 ** 
awesomeness -0.88116    0.03658 -24.091  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3807 on 98 degrees of freedom
Multiple R-squared:  0.8555,    Adjusted R-squared:  0.8541 
F-statistic: 580.4 on 1 and 98 DF,  p-value: < 2.2e-16
abline(fit)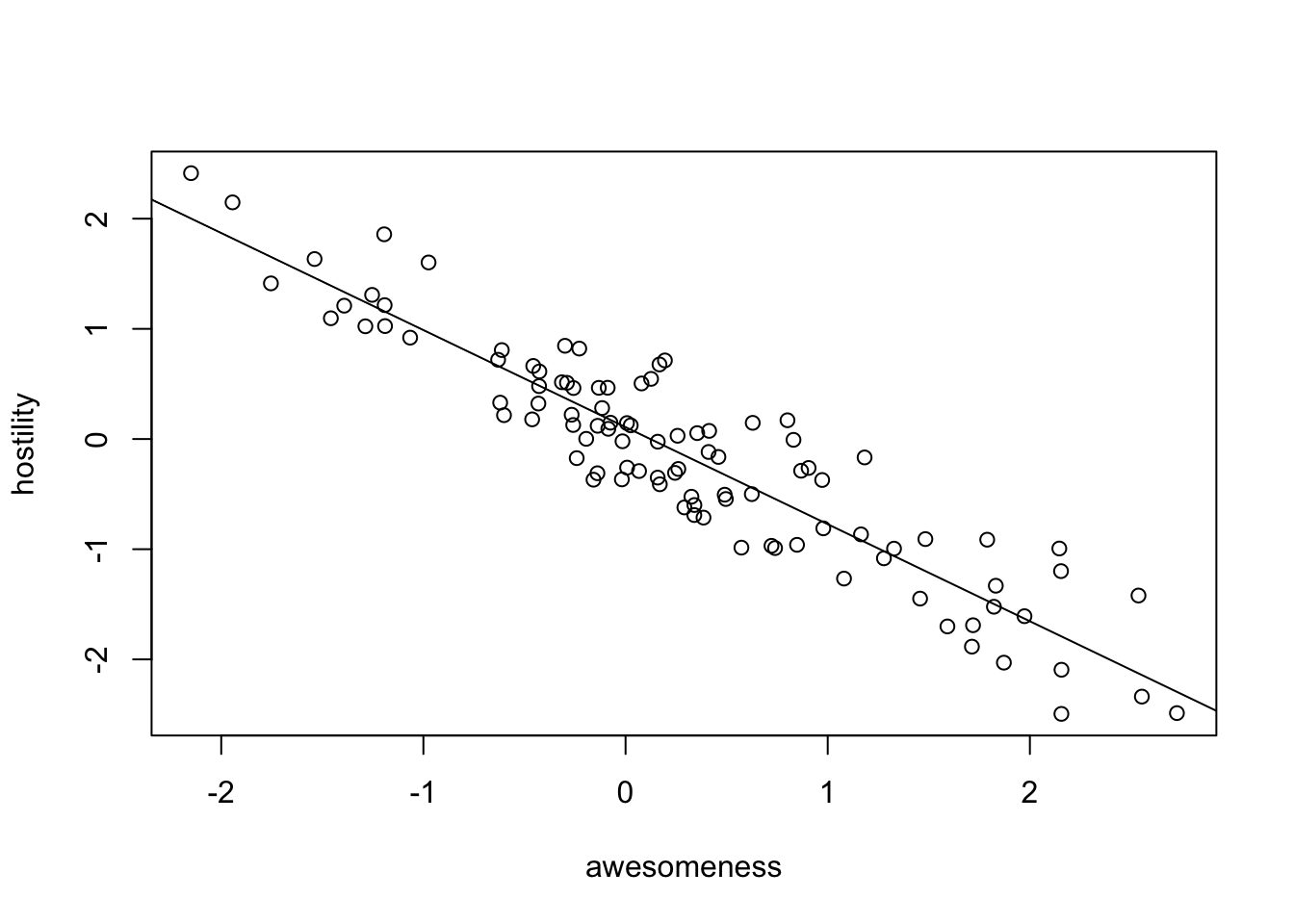

Check for phylogenetic signal in residuals.

# Calculate weight matrix for phylogenetic distance.
w = 1/cophenetic(anolisTree)
diag(w) = 0

Moran.I(residuals(fit), w)
$observed
[1] 0.05067625

$expected
[1] -0.01010101

$sd
[1] 0.00970256

$p.value
[1] 3.751199e-10

Conclusion: signal in the residuals, a normal lm will not work.

You can also check with DHARMa, using this works also for GLMMs

res = simulateResiduals(fit)
testSpatialAutocorrelation(res, distMat = cophenetic(anolisTree))

    DHARMa Moran's I test for distance-based autocorrelation

data:  res
observed = 0.0509093, expected = -0.0101010, sd = 0.0097304, p-value =
3.609e-10
alternative hypothesis: Distance-based autocorrelation

An old-school method to deal with the problem are the so-called Phylogenetically Independent Contrasts (PICs) (Felsenstein, J. (1985) “Phylogenies and the comparative method”. American Naturalist, 125, 1–15.). The idea here is to transform your data in a way that an lm is still appropriate. For completeness, I show the method here.

# Extract columns.
host = anolisData[, "hostility"]
awe = anolisData[, "awesomeness"]

# Give them names.
names(host) = names(awe) = rownames(anolisData)

# Calculate PICs.
hPic = pic(host, anolisTree)
Warning in pic(host, anolisTree): the names of argument 'x' and the tip labels
of the tree did not match: the former were ignored in the analysis.
aPic = pic(awe, anolisTree)
Warning in pic(awe, anolisTree): the names of argument 'x' and the tip labels of
the tree did not match: the former were ignored in the analysis.
# Make a model.
picModel = lm(hPic ~ aPic - 1)

summary(picModel) # Yes, significant.

Call:
lm(formula = hPic ~ aPic - 1)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.30230 -0.23485  0.06003  0.34772  0.92222 

Coefficients:
     Estimate Std. Error t value Pr(>|t|)    
aPic -0.91964    0.03887  -23.66   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4263 on 98 degrees of freedom
Multiple R-squared:  0.851, Adjusted R-squared:  0.8495 
F-statistic: 559.9 on 1 and 98 DF,  p-value: < 2.2e-16
# plot results.
plot(hPic ~ aPic)
abline(a = 0, b = coef(picModel))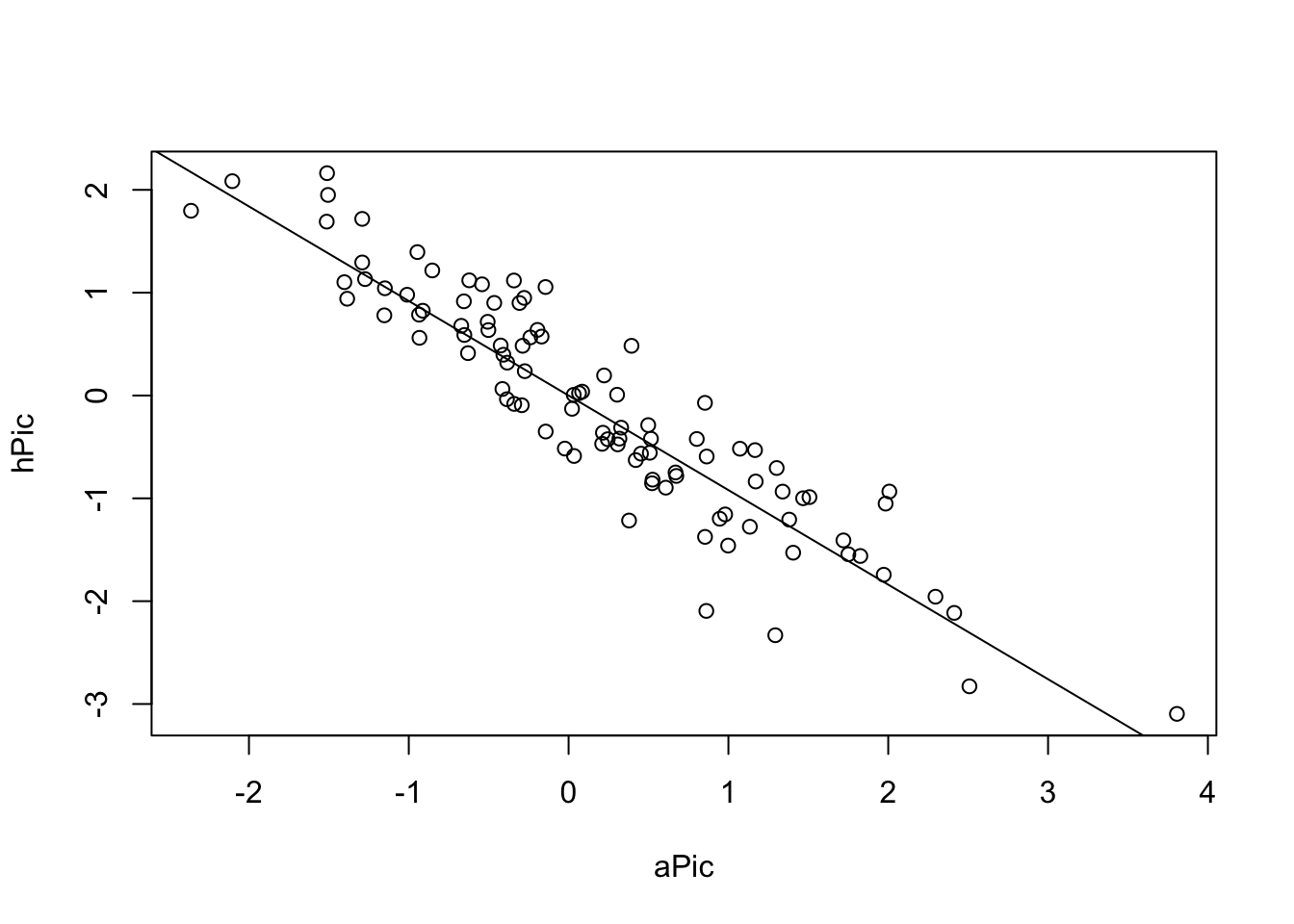

Now, new school, with a PGLS

pglsModel = gls(hostility ~ awesomeness,
                 correlation = corBrownian(phy = anolisTree, form =~ species),
                 data = anolisData, method = "ML")
summary(pglsModel)
Generalized least squares fit by maximum likelihood
  Model: hostility ~ awesomeness 
  Data: anolisData 
       AIC      BIC    logLik
  42.26092 50.07643 -18.13046

Correlation Structure: corBrownian
 Formula: ~species 
 Parameter estimate(s):
numeric(0)

Coefficients:
                 Value  Std.Error    t-value p-value
(Intercept)  0.1158895 0.12500397   0.927087  0.3562
awesomeness -0.9196414 0.03886501 -23.662451  0.0000

 Correlation: 
            (Intr)
awesomeness -0.065

Standardized residuals:
        Min          Q1         Med          Q3         Max 
-1.49512017 -0.75193433 -0.06672209  0.56527753  2.04613817 

Residual standard error: 0.4220369 
Degrees of freedom: 100 total; 98 residual
coef(pglsModel)
(Intercept) awesomeness 
  0.1158895  -0.9196414 
plot(hostility ~ awesomeness, data = anolisData)
abline(pglsModel, col = "red")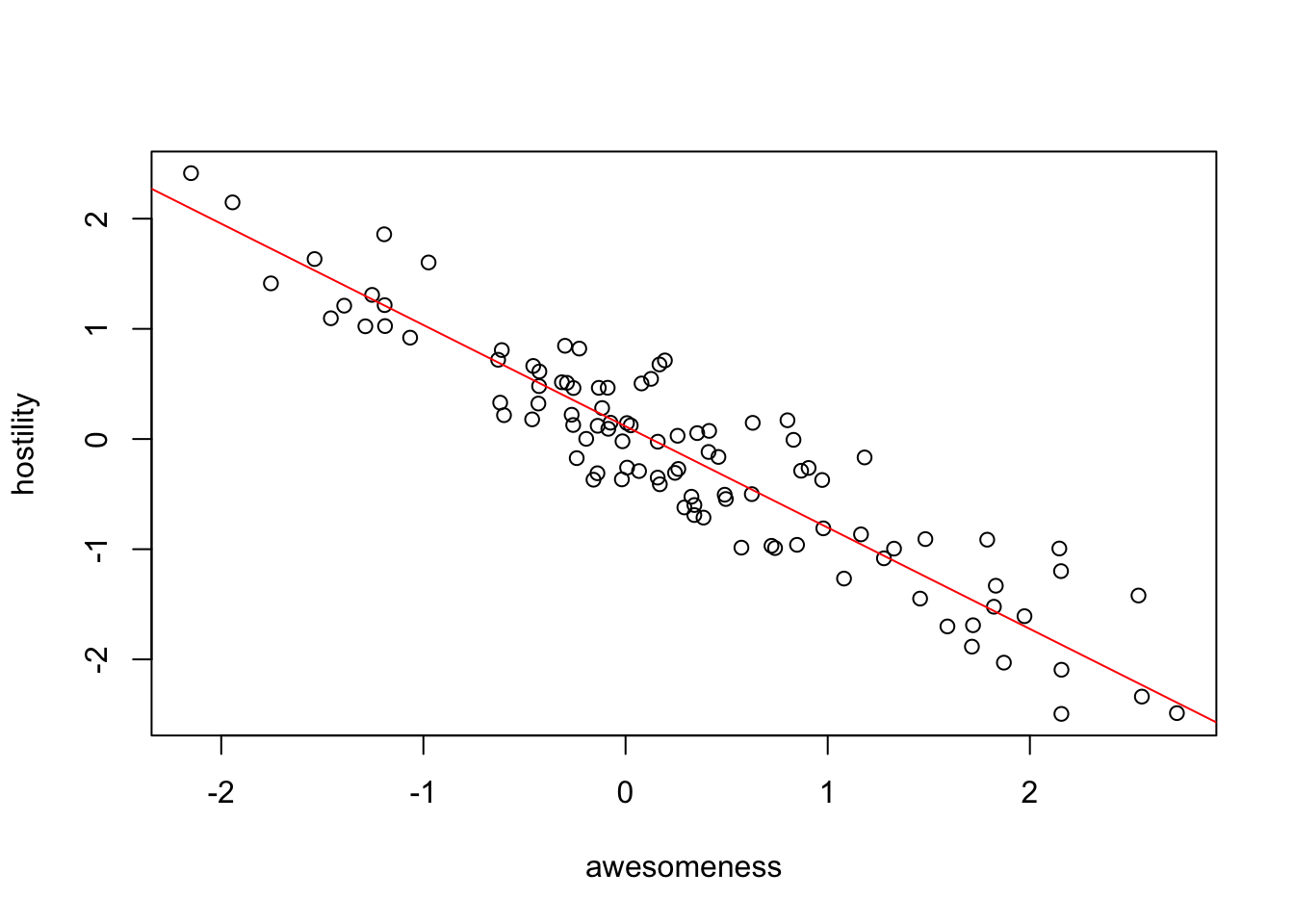

OK, same result, but PGLS is WAY more flexible than PICs. For example, we can include a discrete predictor:

pglsModel2 = gls(hostility ~ ecomorph,
                    correlation = corBrownian(phy = anolisTree, form =~ species),
                    data = anolisData, method = "ML")
summary(pglsModel2)
Generalized least squares fit by maximum likelihood
  Model: hostility ~ ecomorph 
  Data: anolisData 
       AIC     BIC    logLik
  235.1126 255.954 -109.5563

Correlation Structure: corBrownian
 Formula: ~species 
 Parameter estimate(s):
numeric(0)

Coefficients:
                 Value Std.Error    t-value p-value
(Intercept)  0.2280018 0.3630767  0.6279713  0.5316
ecomorphGB  -0.2737370 0.2128984 -1.2857635  0.2017
ecomorphT   -0.2773801 0.3872137 -0.7163490  0.4756
ecomorphTC  -0.5457771 0.2449466 -2.2281475  0.0283
ecomorphTG  -0.2645627 0.2084928 -1.2689297  0.2076
ecomorphTW  -0.5388436 0.2370223 -2.2733878  0.0253
ecomorphU   -0.3013944 0.2264264 -1.3310922  0.1864

 Correlation: 
           (Intr) ecmrGB ecmrpT ecmrTC ecmrTG ecmrTW
ecomorphGB -0.385                                   
ecomorphT  -0.276  0.360                            
ecomorphTC -0.369  0.626  0.349                     
ecomorphTG -0.426  0.638  0.431  0.608              
ecomorphTW -0.372  0.626  0.377  0.588  0.641       
ecomorphU  -0.395  0.597  0.394  0.587  0.647  0.666

Standardized residuals:
        Min          Q1         Med          Q3         Max 
-2.57909973 -0.62394508  0.03716963  0.49997446  2.33859983 

Residual standard error: 1.05295 
Degrees of freedom: 100 total; 93 residual
anova(pglsModel2)
Denom. DF: 93 
            numDF   F-value p-value
(Intercept)     1 0.0555807  0.8141
ecomorph        6 1.2170027  0.3046
# We can even include multiple predictors:

pglsModel3 = gls(hostility ~ ecomorph * awesomeness,
                correlation = corBrownian(phy = anolisTree, form =~ species),
                data = anolisData, method = "ML")
summary(pglsModel3)
Generalized least squares fit by maximum likelihood
  Model: hostility ~ ecomorph * awesomeness 
  Data: anolisData 
       AIC      BIC    logLik
  53.36917 92.44673 -11.68459

Correlation Structure: corBrownian
 Formula: ~species 
 Parameter estimate(s):
numeric(0)

Coefficients:
                            Value  Std.Error    t-value p-value
(Intercept)             0.2740102 0.14336154   1.911323  0.0593
ecomorphGB             -0.2079698 0.08757937  -2.374644  0.0198
ecomorphT              -0.1751884 0.15478802  -1.131795  0.2609
ecomorphTC             -0.2030466 0.10752002  -1.888454  0.0623
ecomorphTG             -0.1260964 0.08339737  -1.511994  0.1342
ecomorphTW             -0.1600076 0.09700188  -1.649531  0.1027
ecomorphU              -0.1244498 0.09457082  -1.315943  0.1917
awesomeness            -1.0131496 0.08971063 -11.293529  0.0000
ecomorphGB:awesomeness  0.0750120 0.08289316   0.904924  0.3680
ecomorphT:awesomeness   0.1373797 0.11770513   1.167152  0.2464
ecomorphTC:awesomeness  0.1161086 0.11490811   1.010447  0.3151
ecomorphTG:awesomeness  0.1666831 0.09824670   1.696577  0.0934
ecomorphTW:awesomeness  0.0120495 0.11532810   0.104480  0.9170
ecomorphU:awesomeness   0.0283477 0.10510376   0.269711  0.7880

 Correlation: 
                       (Intr) ecmrGB ecmrpT ecmrTC ecmrTG ecmrTW ecmrpU awsmns
ecomorphGB             -0.398                                                 
ecomorphT              -0.289  0.372                                          
ecomorphTC             -0.361  0.598  0.357                                   
ecomorphTG             -0.435  0.647  0.447  0.579                            
ecomorphTW             -0.377  0.644  0.391  0.579  0.657                     
ecomorphU              -0.403  0.589  0.424  0.546  0.658  0.666              
awesomeness            -0.104  0.123  0.045  0.078  0.046  0.005  0.108       
ecomorphGB:awesomeness  0.129 -0.280 -0.095 -0.171 -0.151 -0.191 -0.184 -0.682
ecomorphT:awesomeness   0.082 -0.085 -0.074 -0.071 -0.036 -0.011 -0.111 -0.716
ecomorphTC:awesomeness  0.102 -0.120 -0.092 -0.359 -0.079 -0.091 -0.136 -0.695
ecomorphTG:awesomeness  0.090 -0.073 -0.023 -0.058 -0.056 -0.036 -0.140 -0.811
ecomorphTW:awesomeness  0.051 -0.124  0.029 -0.054 -0.023 -0.052 -0.006 -0.666
ecomorphU:awesomeness   0.101 -0.129 -0.129 -0.143 -0.133 -0.122 -0.283 -0.672
                       ecmGB: ecmrT: ecmTC: ecmTG: ecmTW:
ecomorphGB                                               
ecomorphT                                                
ecomorphTC                                               
ecomorphTG                                               
ecomorphTW                                               
ecomorphU                                                
awesomeness                                              
ecomorphGB:awesomeness                                   
ecomorphT:awesomeness   0.516                            
ecomorphTC:awesomeness  0.519  0.530                     
ecomorphTG:awesomeness  0.611  0.684  0.609              
ecomorphTW:awesomeness  0.535  0.536  0.482  0.569       
ecomorphU:awesomeness   0.515  0.535  0.644  0.626  0.480

Standardized residuals:
       Min         Q1        Med         Q3        Max 
-1.6656909 -0.7164061 -0.1305515  0.6718348  1.7699106 

Residual standard error: 0.3956912 
Degrees of freedom: 100 total; 86 residual
anova(pglsModel3)
Denom. DF: 86 
                     numDF  F-value p-value
(Intercept)              1   0.3640  0.5479
ecomorph                 6   7.9691  <.0001
awesomeness              1 517.8319  <.0001
ecomorph:awesomeness     6   0.8576  0.5295

We can also assume that the error structure follows an Ornstein-Uhlenbeck model rather than Brownian motion. When trying this, however, I noted that the model does not converge due to a scaling problem. We can do a quick fix by making the branch lengths longer. This will not affect the analysis other than rescaling a nuisance parameter.

tempTree = anolisTree
tempTree$edge.length = tempTree$edge.length * 100
pglsModelLambda = gls(hostility ~ awesomeness,
                      correlation = corPagel(1, phy = tempTree, fixed = FALSE,
                                             form =~ species),
                      data = anolisData, method = "ML")
summary(pglsModelLambda)
Generalized least squares fit by maximum likelihood
  Model: hostility ~ awesomeness 
  Data: anolisData 
       AIC      BIC    logLik
  43.64714 54.06782 -17.82357

Correlation Structure: corPagel
 Formula: ~species 
 Parameter estimate(s):
 lambda 
1.01521 

Coefficients:
                 Value  Std.Error    t-value p-value
(Intercept)  0.1170472 0.12862370   0.909997  0.3651
awesomeness -0.9248858 0.03870928 -23.893129  0.0000

 Correlation: 
            (Intr)
awesomeness -0.062

Standardized residuals:
        Min          Q1         Med          Q3         Max 
-1.46625592 -0.74557818 -0.06456682  0.54645141  2.02371257 

Residual standard error: 0.4317018 
Degrees of freedom: 100 total; 98 residual
pglsModelOU = gls(hostility ~ awesomeness,
                   correlation = corMartins(1, phy = tempTree, form =~ species),
                   data = anolisData)
summary(pglsModelOU)
Generalized least squares fit by REML
  Model: hostility ~ awesomeness 
  Data: anolisData 
      AIC      BIC    logLik
  50.7625 61.10237 -21.38125

Correlation Structure: corMartins
 Formula: ~species 
 Parameter estimate(s):
      alpha 
0.003194918 

Coefficients:
                 Value Std.Error    t-value p-value
(Intercept)  0.1179388 0.4300640   0.274236  0.7845
awesomeness -0.9148437 0.0384949 -23.765320  0.0000

 Correlation: 
            (Intr)
awesomeness -0.02 

Standardized residuals:
        Min          Q1         Med          Q3         Max 
-1.11558553 -0.54574106 -0.05696661  0.40461428  1.48285458 

Residual standard error: 0.5740297 
Degrees of freedom: 100 total; 98 residual

Other example: http://schmitzlab.info/pgls.html.

For fitting PGLS with various models, you should also consider the caper package.

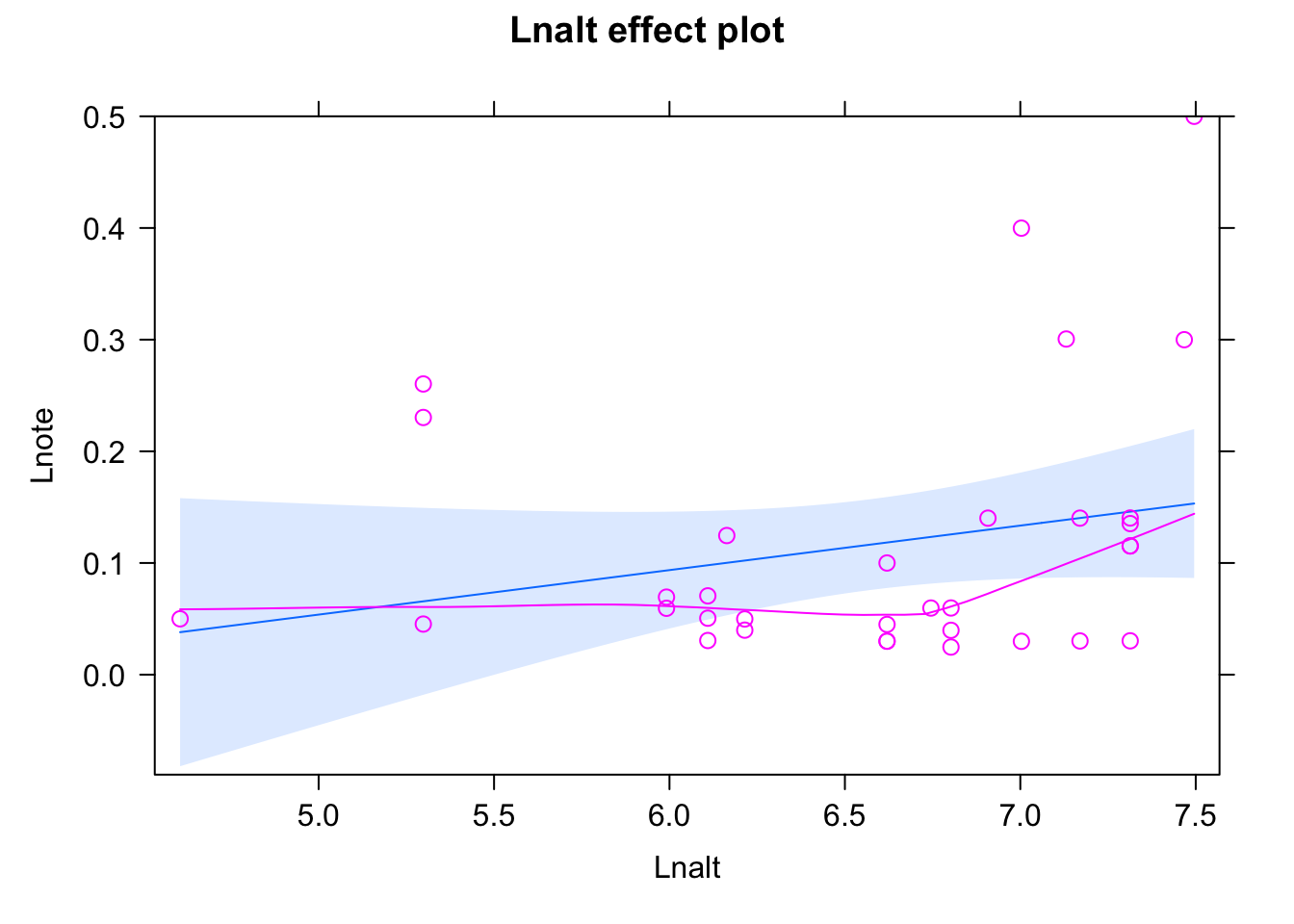
11.4.1 Exercise - Does bird song change with altitude?

11.4.1.1 Excercise

Caution

The following exercise uses data from a study by Corboda et al., 2017, which examined the influence of environmental factors on the evolution of song in an group of Asian bird species called “barbets.” The following code cleans the raw data available from the EcoData package:

library(ape)
library(EcoData)

dat = barbetData
tree = barbetTree

dat$species = row.names(dat)
plot(tree)

# dropping species in the phylogeny for which we don't have data
obj<-geiger::name.check(tree,dat)
reducedTree<-drop.tip(tree, obj$tree_not_data)
geiger::name.check(reducedTree,dat)
[1] "OK"

Task: Check if there is a relationship between altitude at which a species is found and the length of the note in its song, which uses the variables Lnote~Lnalt

plot(Lnote~Lnalt, data = dat)

fit <- lm(Lnote~ scale(Lnalt), data = dat)
summary(fit)

Call:
lm(formula = Lnote ~ scale(Lnalt), data = dat)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.11597 -0.06798 -0.03097  0.01019  0.34676 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   0.11652    0.01994   5.844 1.91e-06 ***
scale(Lnalt)  0.02870    0.02025   1.418    0.166    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1145 on 31 degrees of freedom
Multiple R-squared:  0.06087,   Adjusted R-squared:  0.03058 
F-statistic: 2.009 on 1 and 31 DF,  p-value: 0.1663
library(effects)
Loading required package: carData
lattice theme set by effectsTheme()
See ?effectsTheme for details.
plot(allEffects(fit,partial.residuals = T))
Warning in Analyze.model(focal.predictors, mod, xlevels, default.levels, : the
predictor scale(Lnalt) is a one-column matrix that was converted to a vector

Bit of a misfit, to get a good fit, after playing around, I logged the response and added a quadratic and a cubic effect - you can probably also find other solutions.

fit <- lm(log(Lnote) ~ scale(Lnalt) + I(scale(Lnalt)^2) + I(scale(Lnalt)^3), data = dat)
summary(fit)

Call:
lm(formula = log(Lnote) ~ scale(Lnalt) + I(scale(Lnalt)^2) + 
    I(scale(Lnalt)^3), data = dat)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.54583 -0.34238 -0.05857  0.41449  1.81049 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)       -3.04435    0.19067 -15.967 6.64e-16 ***
scale(Lnalt)      -0.02132    0.22516  -0.095  0.92520    
I(scale(Lnalt)^2)  0.76725    0.21638   3.546  0.00135 ** 
I(scale(Lnalt)^3)  0.27479    0.10296   2.669  0.01233 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.7305 on 29 degrees of freedom
Multiple R-squared:  0.3376,    Adjusted R-squared:  0.2691 
F-statistic: 4.928 on 3 and 29 DF,  p-value: 0.006911
plot(allEffects(fit,partial.residuals = T))
Warning in Analyze.model(focal.predictors, mod, xlevels, default.levels, : the
predictors scale(Lnalt), I(scale(Lnalt)^2), I(scale(Lnalt)^3) are one-column
matrices that were converted to vectors

Warning in Analyze.model(focal.predictors, mod, xlevels, default.levels, : the
predictors scale(Lnalt), I(scale(Lnalt)^2), I(scale(Lnalt)^3) are one-column
matrices that were converted to vectors

Warning in Analyze.model(focal.predictors, mod, xlevels, default.levels, : the
predictors scale(Lnalt), I(scale(Lnalt)^2), I(scale(Lnalt)^3) are one-column
matrices that were converted to vectors

Now, with a more complex polynomial for Lnalt, how to we see if there is an overall effect of Lnalt? Easiest option is to do a LRT:

fit0 = lm(log(Lnote)~ 1, data = dat)
anova(fit0, fit)
Analysis of Variance Table

Model 1: log(Lnote) ~ 1
Model 2: log(Lnote) ~ scale(Lnalt) + I(scale(Lnalt)^2) + I(scale(Lnalt)^3)
  Res.Df    RSS Df Sum of Sq      F   Pr(>F)   
1     32 23.366                                
2     29 15.477  3    7.8893 4.9276 0.006911 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Check residuals for phylogenetic correlation

w = 1/cophenetic(reducedTree)
diag(w) = 0
Moran.I(residuals(fit), w)
$observed
[1] -0.06427062

$expected
[1] -0.03125

$sd
[1] 0.03427974

$p.value
[1] 0.3354125

Nothing! So we could leave the model as it is. Just for completeness, fit the same comparison with a PGLS, effect remains significant, but p-value a bit larger.

fit <- gls(Lnote~ scale(Lnalt) * I(scale(Lnalt)^2), 
           correlation = corBrownian(phy = reducedTree, 
                                     form =~ species), data = dat, 
           method = "ML")
summary(fit)
Generalized least squares fit by maximum likelihood
  Model: Lnote ~ scale(Lnalt) * I(scale(Lnalt)^2) 
  Data: dat 
        AIC       BIC   logLik
  -76.95977 -69.47723 43.47988

Correlation Structure: corBrownian
 Formula: ~species 
 Parameter estimate(s):
numeric(0)

Coefficients:
                                    Value  Std.Error   t-value p-value
(Intercept)                    0.14433555 0.07391392 1.9527520  0.0606
scale(Lnalt)                   0.02481932 0.02700222 0.9191586  0.3656
I(scale(Lnalt)^2)              0.03434214 0.02114728 1.6239510  0.1152
scale(Lnalt):I(scale(Lnalt)^2) 0.01160067 0.01076432 1.0776963  0.2901

 Correlation: 
                               (Intr) scl(L) I((L)^
scale(Lnalt)                    0.224              
I(scale(Lnalt)^2)              -0.286 -0.565       
scale(Lnalt):I(scale(Lnalt)^2) -0.230 -0.791  0.861

Standardized residuals:
       Min         Q1        Med         Q3        Max 
-1.5858745 -0.8709001 -0.7491330 -0.3869937  2.0469866 

Residual standard error: 0.1188854 
Degrees of freedom: 33 total; 29 residual

Btw, did you notice that neither Lnalt has a significant effect - so is there no dependence on Lnalt? Because we have the linear and quadaratic effect, the best way to answer this is to run an ANOVA:

fit0 <- gls(Lnote~ 1, 
           correlation = corBrownian(phy = reducedTree, 
                                     form =~ species), data = dat, 
           method = "ML")

anova(fit0, fit)
     Model df       AIC       BIC   logLik   Test  L.Ratio p-value
fit0     1  2 -73.47388 -70.48087 38.73694                        
fit      2  5 -76.95977 -69.47723 43.47988 1 vs 2 9.485883  0.0235

which tells us that Lnalt has a significant effect, even though we can’t reject that either the linear or the quadrart term is zero.

Addition: what would happen if we do the same with a misspecified model? Have a look at the p-values of the fitted models. Can you explain what’s going on here?

fit <- lm(Lnote~ scale(Lnalt), data = dat)
summary(fit)

Call:
lm(formula = Lnote ~ scale(Lnalt), data = dat)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.11597 -0.06798 -0.03097  0.01019  0.34676 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   0.11652    0.01994   5.844 1.91e-06 ***
scale(Lnalt)  0.02870    0.02025   1.418    0.166    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1145 on 31 degrees of freedom
Multiple R-squared:  0.06087,   Adjusted R-squared:  0.03058 
F-statistic: 2.009 on 1 and 31 DF,  p-value: 0.1663
plot(allEffects(fit, partial.residuals = T))
Warning in Analyze.model(focal.predictors, mod, xlevels, default.levels, : the
predictor scale(Lnalt) is a one-column matrix that was converted to a vector

w = 1/cophenetic(reducedTree)
diag(w) = 0
Moran.I(residuals(fit), w)
$observed
[1] -0.05831654

$expected
[1] -0.03125

$sd
[1] 0.0334855

$p.value
[1] 0.4189142
fit <- gls(Lnote~ scale(Lnalt), 
           correlation = corBrownian(phy = reducedTree, 
                                     form =~ species), data = dat, 
           method = "ML")
summary(fit)
Generalized least squares fit by maximum likelihood
  Model: Lnote ~ scale(Lnalt) 
  Data: dat 
        AIC      BIC   logLik
  -77.67763 -73.1881 41.83881

Correlation Structure: corBrownian
 Formula: ~species 
 Parameter estimate(s):
numeric(0)

Coefficients:
                  Value  Std.Error  t-value p-value
(Intercept)  0.18020988 0.07194706 2.504757  0.0177
scale(Lnalt) 0.03941982 0.01556802 2.532103  0.0166

 Correlation: 
             (Intr)
scale(Lnalt) 0.15  

Standardized residuals:
       Min         Q1        Med         Q3        Max 
-1.5260202 -1.0620664 -0.7067039 -0.4679653  2.1556803 

Residual standard error: 0.1249469 
Degrees of freedom: 33 total; 31 residual

The observation is that the PGLS effect estimate is significant while normal lm is not. The reason is probably that the PGLS is re-weighting residuals, and it seems that in this case, the re-weighting is changing the slope. What we learn by this example is that a PGLS can increase significance, and in this case I would argue wrongly so, as we have no indication that there is a phylogenetic signal. I would therefore NOT recommend to blindly fit PGLS, but rather test first if a PGLS is needed, and only then apply.

11.5 Multivariate GLMs

In the recent years, multivariate GLMs, in particular the multivariate probit model, and latent variable versions thereof, have become popular for the analysis of community data. The keyword here is “joint species distribution models” (jSDMs).

Briefly, what we want a jSDM to do is to fit a vector of responses (could be abundance or presence / absence data) as a function of environmental predictors and a covariance between the responses. The model is thus

\[ y \sim f(x) + \Sigma \] where y is a response vector, f(x) is a matrix with effects, and \(\Sigma\) is a covariance matrix that we want to estimate.

You can fit these models directly in lme4 or glmmTMB via implementing an RE per species

lme4(abundance ~ 0 + species + env:species + (0+species|site)
glmmTMB(abundance ~ 0 + species + env:species + (0+species|site)

however, these so-called full-rank models have a lot of degrees of freedom and are slow to compute if the number of species gets large. It has therefore become common to fit rank-reduced versions of the these models using a latent-variable reparameterization of the model above. A latent-variable version of this model can be fit in glmmTMB via this syntax

glmmTMB(abundance ~ 0 + species + env:species + rr(Species + 0|id, d = 2))

The parameter d controlls the number of latent variables.

Of course, there are many more specialized packages for fitting latent-variable jSDMs in R right now, including hmsc, gllvm or sjSDM, but I find it nice to set this models in the general topic of correlations, and realize that we can fit them with the same methods and packages as for all other correlation structures.